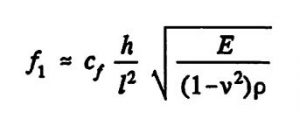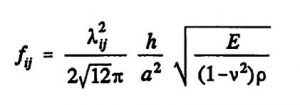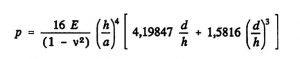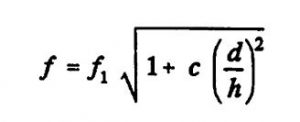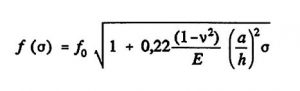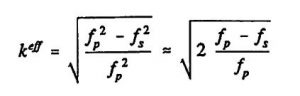Finite-Elemente-Modellierung frequenz-analoger Sensoren
HSG-IMIT
Institut für Mikro- und Informationstechnik der Hahn-Schickard-Gesellschaft
für Angewandte Forschung e.V.,
Villingen-Schwenningen
2.1 Einleitung
2.1.1 Funktionsprinzip resonanter Sensoren
Das Prinzip eines resonanten Sensors beruht auf der Abhängigkeit der Eigenfrequenz des Resonators von einer äußeren physikalischen Größe (z.B. Druck, Kraft, Temperatur), indem der Spannungszustand beeinflußt oder die Trägheit des Resonators über eine Massenbelegung verändert wird. Die Resonanzfrequenz stellt als Meßgröße ein quasi-digitales Ausgangssignal dar. Der Sensor wird einerseits durch seine passiven Resonator-Eigenschaften wie Eigenfrequenz, Schwingungsmode und der Kopplung zur Meßgröße, andererseits durch die Eigenschaften der Schwingungsanregung und -detektion, beispielsweise der Modenselektivität, der Effizienz der Energie-Einkopplung und der Auflösung des Abfrage-Systems charakterisiert.
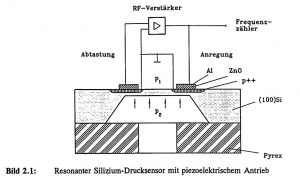
Im Folgenden soll das frequenzanaloge Funktionsprinzip stellvertretend am Beispiel eines resonanten, mikro-mechanischen Drucksensors aufgezeigt werden, der in Bild 2.1 schematisch dargestellt ist. Die Anregung wird durch eine piezo-elektrische Dünnschicht (hier: Zinkoxid) bewerkstelligt, die mit Hilfe des transversalen piezo-elektrischen Effektes bei Anlegen einer elektrischen Wechselspannung infolge Dehnungen und Kontraktionen auf der Membranoberfläche Biegemomente erzeugt und somit zu periodischen Membran-Auslenkungen führt. Infolge einer Druckdifferenz zwischen Unter- und Oberseite der Membran wird der Silizium-Resonator deformiert. Der Betrag der statischen Auslenkung ist ein Vielfaches größer als die dynamische Schwingungsamplitude. Bei genügend großer statischer Auslenkung stellen sich durch Reaktionskräfte Membran-Spannungen ein, die zu einer Versteifung des Resonators führen, so daß sich die Resonanzfrequenz analog zur Meßgröße ändert. Wird umgekehrt der piezo-elektrische Effekt auch zur Schwingungsdetektion genutzt, so kann mit einer geeigneten Auswerteschaltung der Sensor in Eigenresonanz betrieben und die Frequenzänderung über einen Frequenzzähler ausgelesen werden.
Bild 2.1: Resonanter Silizium-Drucksensor mit piezoelektrischem Antrieb
2.1.2 Materialeigenschaften mikromechanischer Werkstoffe
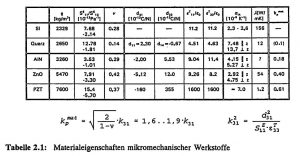
In Tabelle 2.1 sind die mechanischen, thermischen, piezo- und dielektrischen Materialeigenschaften einiger wichtiger in der Mikromechanik verwendeter Werkstoffe zusammen-gestellt. Als Substratmaterial wird für resonante Sensoren neben einkristallinem Silizium auch einkristalliner Quarz verwendet. Da Silizium nicht piezo-elektrisch ist, werden z.B. Aluminiumnitrid (AlN) und Zinkoxid (ZnO) als piezo-elektrisch aktive Wandler-Schichten eingesetzt. Im Vergleich zu den in Dünnschicht-Technologie (Sputter-Prozeß) hergestellten polykristallinen Materialien AlN und ZnO zeichnen sich PZT-Piezokeramiken (Blei-Zirkonat-Titanat) durch extrem hohe, einkristallines Quarz hingegen durch relativ niedrige piezo-elektrische Kopplungskoeffizienten d_ij aus. Ein Maß für die Effizienz der Umwandlung von elektrischer in mechanische Energie stellt der elektro-mechanische Kopplungsfaktor dar. Der effektive Kopplungsfaktor k_eff setzt sich aus einem material- und einem geometrieabhängigen Anteil zusammen und kann nur mit Hilfe gekoppelter FE-Berechnungen für eine gegebene Resonator-Geometrie ermittelt werden.
Die materialabhängigen transversalen und planaren Kopplungsfaktoren k_31 bzw. k_pmat für reine Transversal- bzw. Planar-Schwinger sind von dem mechanischen Steifigkeitskoeffizienten S_11E, der Poissonzahl v (= – S_12/S_11), sowie den piezo- und di-elektrischen Konstanten d_31 bzw. e_33T der piezo-elektrischen Dünnschicht (Zusammenhänge siehe Tabelle 2.1) abhängig [VIB 81]. Da die Materialparameter mikrotechnisch hergestellter Schichtsysteme stark vom technologischen Herstellungsprozeß beeinflußt werden, unterscheiden sie sich u.U. erheblich von denen des Festkörper-Materials (Bulk) und weisen in der Regel prozeß-technisch bedingte innere Spannungen auf. Die angegebenen Materialdaten beziehen sich lediglich für Aluminiumnitrid auf einige Mikrometer dünne Schichten [Fra 88], die anderen Angaben beziehen sich auf Bulk-Material [LB 82], [Tic 80], [VIB 81].
Tabelle 2.1: Materialeigenschaften mikromechanischer Werkstoffe
2.1.3 Analytische Auslegung von resonanten Sensoren
Für die Anwendung als resonanter Kraft- und Drucksensor kommen insbesondere Biegebalken- und Membran-Resonatoren in Frage. Unter der Annahme idealer Einspann-Bedingungen und homogener, isotroper Material-Eigenschaften lassen sich die Resonanz-Frequenzen und lastabhängigen Frequenzänderungen des Resonators für einfache Schwinger-Geometrien analytisch ermitteln. Durch die analytischen Ansätze kann der Arbeitspunkt resonanter Sensoren, d.h. die Grundresonanzfrequenz und die Meßgrößen-Empfindlichkeit, über eine geeignete Wahl der geometrischen Abmessungen eingestellt werden.
Die Resonanzfrequenzen für die Biegeschwingungen sind von den geometrischen Dimensionen, Resonatorlänge l und -dicke h, der Einspannungsart sowie der Materialparameter, Elastizitätsmodul E, Poissonzahl v und Materialdichte ρ abhängig. Für die Resonanzfrequenz der Grundbiegeschwingung gilt [Alb 82]:
(Gleichung 1)
Die Proportionalitätskonstante c_f ist von der Resonator-Geometrie und der Schwingungsmode abhängig und beträgt für doppelseitig eingespannte Biegebalken etwa 1,028. Die Kraftempfindlichkeit von Balken-Resonatoren wird in Kapitel 5 diskutiert.
Die in der Literatur für Membranen angegebenen analytischen Zusammenhänge für den Auslenkungs- und Spannungszustand, sowie die Resonanzfrequenzen beruhen auf der Kirchhoffschen Platten- und Schalen-Theorie und gehen von der Annahme ebener Objekte aus, deren laterale Abmessungen wesentlicher größer als deren Dicke ist. Bei der Ermittlung der Eigenfrequenzen und Schwingungsformen werden verschiedene Näherungsverfahren (z.B. [You 50]) verwendet. Für die Resonanzfrequenzen f_ij ebener Membranen gilt [Ble 84]:
wobei:
- E, v : isotroper Elastizitätsmodul, Poissonzahl
- a,h : Membranseitenlänge, -dicke
- i,j : Anzahl der Halbwellen in x- bzw. y- Richtung
- ρ : Dichte (Materialhomogenität angenommen)
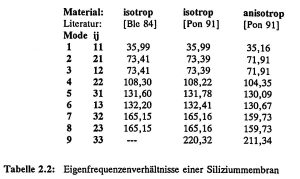
Die Konstante λ ist von den Einspannbedingungen und dem Seitenverhältnis der Membran abhängig und wird auch als normierte Eigenfrequenz für den jeweiligen Schwingungsmode bezeichnet. Tabelle 2.2 enthält eine Zusammenstellung der normierten Eigenfrequenzen λ_ij einer fest eingespannten, quadratischen, homogenen Membran, wobei in [Pon 91] auch die Eigenfrequenzen für anisotropes Materialverhalten angegeben werden.
Tabelle 2.2: Eigenfrequenzen-Verhältnisse einer Siliziummembran
Für die Eigenfrequenzverschiebung als Folge einer Druckeinwirkung ergibt sich eine Überlagerung eines statischen und dynamischen Problems. Im ersten Schritt wird die Membran-Mittenauslenkung als Funktion des einwirkenden Druckes ermittelt, im zweitem Schritt die Frequenzverschiebung als Funktion der Membran-Auslenkung. Die Überlagerung ergibt die Frequenz-Verschiebung als Funktion des einwirkenden Druckes. In der Literatur wird von verschiedenen Ansätzen ausgegangen, bei denen lineare Zusammenhänge für relativ dicke Membranen bei kleinen Auslenkungen bzw. nichtlineare Zusammenhänge für dünne Membranen bei großen Auslenkungen angegeben werden. Für quadratische, fest eingespannte Platten der Dicke h gilt für den nichtlinearen Zusammenhang zwischen einwirkendem Druck p und der Membran-Mittenauslenkung d nach [Cha 87]:
(Gleichung 3)
Diese Gleichung kann mit Hilfe der Lösungsformel nach Kardan aufgelöst und zur Berechnung der Resonanz-Frequenzänderung in Abhängigkeit von der Auslenkung [Utt 87] herangezogen werden:
(Gleichung 4)
Die Konstante c ist von der Einspannung und der Membranform abhängig. Für die Auslegung resonanter Siliziumsensoren, die bei Biegeschwingungen Dehnungen in <110>-Kristallrichtung erfahren, wird für den Elastizitätsmodul E = 168,9 GPa und für die Poissonzahl v = 0,063 angenommen. Die Dichte ρ von Silizium beträgt 2329 kg/m³. Die angegebenen Materialdaten beziehen sich auf Zimmertemperatur.
2.1.4 Numerische Modellierverfahren für resonante Sensoren
Beim Entwurf von mikromechanischen Sensoren kommt der Simulation mit Hilfe der Finite-Elemente-Methode (FEM) eine wichtige Bedeutung zu, da sie bereits in der Entwurfsphase gestattet, auch komplexe Schwinger-Geometrien mit beliebigen Randbedingungen und die technologisch zu realisierenden Funktionsprinzipien unter Berücksichtigung prozeß-technischer Einschränkungen zu modellieren. Als Ausgangswerte für die numerischen Modellrechnungen dienen analytische Abschätzungen, die in der Regel nur für einfache Struktur-Geometrien durchgeführt werden können. Durch Parametervariationen des FE-Modells kann der Einfluß der Schwinger-Geometrie und der Materialeigenschaften der Dünnschichtsysteme vorab studiert werden. Die FE-Methode erlaubt somit resonante, mikromechanische Sensoren geeignet auszulegen und die Sensoreigenschaften gezielt zu optimieren.
Mit Hilfe dynamischer FE-Berechnungen werden die Eigen-Frequenzen und Schwingungsformen (Modalanalyse) verschiedener Sensorstrukturen (Einfach-, Dreifachbalken, Membranen) bestimmt und der Einfluß der zu unter-suchenden Meßgröße ermittelt. Die Berechnung der Druck- bzw. Kraftempfindlichkeit erfolgt durch eine nichtlineare, statische FE-Berechnung, in welcher die durch die Meßgröße hervorgerufene Steifigkeitsänderung des Gesamtsystems bestimmt wird. Die geänderte Struktur-Steifigkeit wird anschließend herangezogen, um die Eigenfrequenzen des Sensors unter dieser Belastung zu ermitteln. Durch einen Vergleich der berechneten Sensorkennlinien mit experimentellen Daten mikro-mechanischer Resonator-Strukturen in Mehrlagenaufbau (sog. Multilayer-Strukturen) kann auf die innere Spannung der Dünnschichten zurück geschlossen werden.
Gekoppelte FE-Berechnungen unter Berücksichtigung der elektromechanischen Wechselwirkung ermöglichen eine gezielte Vorhersage des statischen und dynamischen Verhaltens von piezoelektrisch betriebenen Sensoren. Das Frequenzgangverhalten wird ermittelt, indem das mechanische Amplitudenspektrum und der elektrische Impedanz- und Phasenverlauf in Abhängigkeit der piezoelektrischen Anregung modelliert wird. Insbesondere wurde das Schichtdicken-Verhältnis in Bezug auf die Anregungseffizienz optimiert und die Elektrodengeometrie für eine möglichst selektive Schwingungsanregung abgeleitet.
Der vorliegende Bericht dokumentiert die Möglichkeiten, gekoppelte dynamische FE-Berechnungen im Entwurfsprozeß von resonanten mikromechanischen Sensoren einzusetzen. Ein Vergleich von numerischen und experimentellen Ergebnisse zeigt die erreichbaren Modellierungsgenauigkeiten der FE-Berechnungsmethode auf. Für die Modellierung wurde das kommerziell verfügbare Finite-Elemente Programmsystem ANSYS eingesetzt [SASI].
2.2 Dynamische Eigenschaften mikromechanischer Resonatoren
Aufgrund der verschiedenen Schwinger-Geometrien und der spezifischen Resonator-Charakteristika resonanter Sensoren, wie Materialeigenschaften und Randbedingungen, treten unterschiedliche Schwingungsformen auf. Während bei dünnen Silizium-Membranen aufgrund der Momenten-Anregung nur Biegeschwingungen und deren Oberwellen auftreten, sind bei Quarz-Membranen aufgrund der Kristallstruktur auch überlagerte, komplexe Schwingungsformen (z.B. Dicken-Scherschwingungen, Kapitel 3) möglich. Im Fall von Balkenresonatoren können bei beiden Materialien neben den Biegeschwingungen auch Longitudinal- und Torsionsschwingungen, sowie Überlagerungen dieser Schwingungsformen auftreten.
2.2.1 Quarz-Doppelstimmgabeln
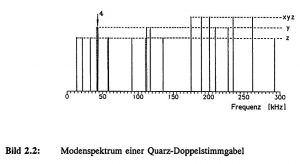
Die Berechnung der Eigenfrequenzen von Quarz-Schwingern erlaubt die Genauigkeit der FE-Methode zu testen, da die Materialeigenschaften von einkristallinem Quarz sehr genau bekannt sind [Bri 85] und keine Verspannungen infolge von Dünnschichten zu beachten sind. Die Biegeresonanzfrequenzen von Kraftsensoren auf der Basis von Quarz-Doppelstimmgabeln (DETF) konnten mit einfachen, zweidimensionalen FE-Modellansätzen mit isotropen Materialverhalten berechnet werden, so daß die Abweichungen zu experimentell gemessenen Werten weniger als 2 % betrugen. Die Modellierung komplexer Schwingungsformen setzt allerdings eine dreidimensionale Formulierung unter Einschluß des anisotropen Material-Verhaltens und der piezoelektrischen Eigenschaften, sowie die Berücksichtigung der elektrischen Abschluß-Bedingungen der Elektroden voraus. In Bild 2.2 ist das Modenspektrum einer idealisierten Quarz-Doppel-Stimmgabel (Stimmgabellänge: 5,0 mm, Stimmgabelbreite: 0,2 mm) dargestellt. Um alle möglichen Bewegungsformen der Quarz-Doppel-Stimmgabel, also auch Torsions- und überlagerte Schwingungsformen zu berechnen, wurde ein 3D-Modell erstellt. Im unteren Frequenzbereich dominieren unterschiedliche Biege-Schwingungen (y-, z-Richtung), während mit steigender Frequenz sich zunehmend Torsions- und überlagerten xyz-Schwingungszustände einstellen.
Bild 2.2: Modenspektrum einer Quarz-Doppelstimmgabel
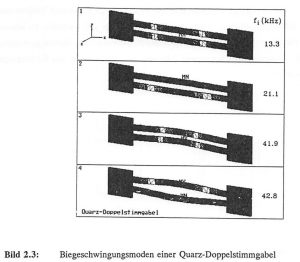
In Bild 2.3 sind die den ersten vier Eigenfrequenzen entsprechenden Schwingungsmoden der Quarz-Doppelstimmgabel (DETF) dargestellt. In der Eigen-Schwingungsmode, in der die Doppelstimmgabel als Kraftsensor betrieben wird, schwingen die Stimmgabel-Stege gegenphasig zueinander, so daß keine Momente in die Befestigungsbereiche ausgekoppelt werden. Die vierte Schwingungsmode weist aufgrund der gegenphasigen Stimmgabelbewegungen die höchste Schwingungsgüte verbunden mit der höchsten Kraftauflösung auf. Bei den höheren Schwingungsmoden wechseln sich symmetrische (phasengleich) und antisymmetrische (180° phasenverschoben) Stimmgabel-Bewegungen ab und die Anzahl der Schwingungsmaxima nimmt zu. Die Doppel-Stimmgabel ist in y-Richtung steifer als in z-Richtung, so daß die transversalen z-Schwingungen bei 13,3 (gleichphasig) und 21,1 kHz (gegenphasig) frequenzmäßig am tiefsten liegen. Die beiden trans-versalen Grundschwingungen in y-Richtung bei 41,9 und 42,8 kHz liegen aufgrund der erhöhten Biegesteifigkeit in y-Richtung frequenzmäßig höher.
Bild 2.3: Biegeschwingungsmoden einer Quarz-Doppelstimmgabel
Bei der Berechnung der Kraftempfindlichkeit von Quarz-Doppelstimmgabeln wird der Sensor mit einer axialen Zugkraft beaufschlagt und die Resonanzfrequenzänderung berechnet. Die Kraftempfindlichkeit des Quarz-Sensors ist abhängig von dem Verhältnis der Stimmgabellänge zur Stimmgabelbreite. Die Kraftempfindlichkeiten wurden für verschiedene Schwingungsmoden berechnet. Die höchste Empfindlichkeit weist die y-A1-Mode mit etwa 1,83 l/N auf, während die Grundmode y-S1 bei 1,64 l/N (y-S1: symmetrische Mode, y-A1: gegenphasige Mode) liegt. Die Kraftempfindlichkeiten der höheren Biege-Schwingungsmoden nehmen stark ab. Messungen an kommerziell erhältlichen Quarz-Doppelstimmgabeln (Micro Crystal, CH-Grenchen), die in der gegenphasigen Mode y-A1 angeregt werden, ergaben einen Wert von etwa 1,42 l/N. Für verschiedene Stimmgabelbreiten wurden die Kraft-Frequenz-Kennlinien berechnet.
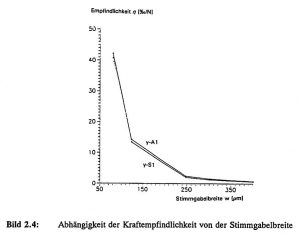
In Bild 2.4 sind die Kraftempfindlichkeiten η der beiden Biegeschwingungsmoden in der Balkenebene in Abhängigkeit der Stimmgabelbreite w dargestellt. Die Stimmgabelbreite wurde von 0,4 bis 0,08 mm variiert und führte zu einer maximalen Empfindlichkeit von etwa 42 l/N für die y-A1-Schwingungsmode. Die Nichtlinearität der Kennlinie beträgt allerdings bei der minimalen Balkenbreite etwa 2,5 % bezogen auf den maximalen Meßbereich (hier: 10 N).
Bild 2.4: Abhängigkeit der Kraftempfindlichkeit von der Stimmgabelbreite
2.2.2 Silizium-Balkenresonatoren mit unterschiedlichen Querschnitten
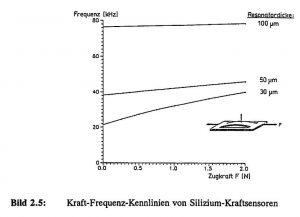
Naßchemisch geätzte Balkenresonatoren in (100)-Silizium weisen einen prismatischen Querschnitt auf. Bei Kraftsensor-Anwendungen werden Stabilisierungsstege (sog. Shunts) in Wafer-Dicke parallel zum schwingenden Balken als Überlastschutz vorgesehen. In Bild 2.5 sind die numerisch berechneten Kraft-Frequenz-Kennlinien von Silizium-Balkenresonatoren in Abhängigkeit der Balken-Dicke für die Grundmode dargestellt.
Bild 2.5: Kraft-Frequenz-Kennlinien von Silizium-Kraftsensoren
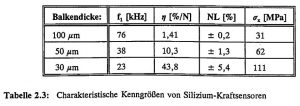
Tabelle 2.3 faßt die charakteristischen Kenngrößen, die Grundresonanzfrequenz f_1, die Kraftempfindlichkeit η, die Kennlinien-Nichtlinearität NL und die maximale Zugspannung σ_x (bei F = 2 N) der berechneten Silizium-Kraftsensoren zusammen.
Tabelle 2.3: Charakteristische Kenngrößen von Silizium-Kraftsensoren
Die Frequenzverschiebung ist abhängig von der Größe der mechanischen Spannung im Resonator, so daß durch eine Änderung des Resonator-Querschnitts die Kraft-Empfindlichkeit erhöht werden kann. Durch Laser-Strukturierung von Silizium in Kombination mit anisotroper Naßätztechnik (siehe auch Kapitel 5) können dreiecksförmige Balken-Querschnitte mit einem spitzen Winkel von 35° in (110)-Silizium hergestellt werden, die bei einer gleichen Kraftbeaufschlagung eine höhere Resonator-Verspannung als prismatische Balken aufweisen [Ala 92].
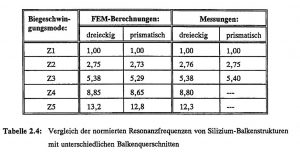
In Tabelle 2.4 sind die numerisch berechneten Resonanzfrequenzvielfachen c_i = f_i / f_1 von Einfach-Balkenstrukturen mit verschiedenen Balkenquerschnitten aus Silizium aufgelistet und Meßwerten gegenübergestellt. Die Frequenzen sind auf die jeweilige Grundmode Z1 normiert. Die verschiedenen Oberschwingungen aus der Balkenebene heraus sind mit Z2 bis Z5 gekennzeichnet. Die Balkenlänge betrug 3 mm, die Breite 200 μm, während die Dicke etwa 70 μm betrug (siehe auch Kapitel 6).
Tabelle 2.4: Vergleich der normierten Resonanzfrequenzen von Silizium-Balkenstrukturen mit unterschiedlichen Balkenquerschnitten
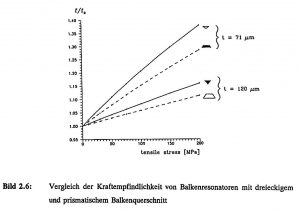
In Bild 2.6 sind die normierten Resonanzfrequenzen von Balkenschwinger mit dreieckigen und prismatischen Balkenquerschnitt in Abhängigkeit der mechanischen Zugspannung im Biegebalken dargestellt. Bei den dreieckigen Balkenquerschnitten wird eine um etwa 30 % höhere Kraftempfindlichkeit als bei den prismatischen erreicht [Ala 92].
Bild 2.6: Vergleich der Kraftempfindlichkeit von Balkenresonatoren mit dreieckigem und prismatischem Balkenquerschnitt
Ein weiterer Gesichtspunkt bei der Auslegung von resonanten Sensor-Geometrien ist die Wahl der günstigsten Resonator-Halterung, um die inneren Dämpfungsbeiträge des Schwingers möglichst gering zu halten. In Kapitel 5 wird über die Realisierung eines resonanten Kraftsensors auf der Basis einer Dreifachbalkenstruktur aus Silizium berichtet. Durch eine Momenten-Kompensation wird eine erhöhte Schwingungsgüte erreicht. Zusätzlich hat eine geeignete Strukturierung der Resonator-Befestigung eine Moden-Entkopplung zur Folge, die sich durch eine verbesserte Moden-Selektivität, d.h. Unimodalität des Resonator-Systems ausdrückt.
2.2.3 Resonante Silizium-Membrandrucksensoren
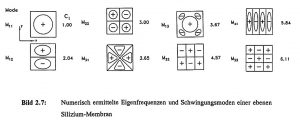
Für die resonante Drucksensoranwendung kommen sowohl ebene als auch strukturierte Membranen aus Silizium (Kapitel 2.1.1) oder Quarz mit piezoelektrischer Anregung in Frage. In Zusammenarbeit mit dem HSG-IMIT hat der Verbundpartner MotoMeter GmbH einen resonanten Quarz-Drucksensor auf der Basis einer strukturierten Membran entwickelt, über dessen Entwurf und Realisierung in Kapitel 3 ausführlich berichtet wird. Der Verbundpartner Robert Bosch GmbH hat resonante Drucksensoren in Silizium hergestellt, die in enger Kooperation mit dem HSG-IMIT modelliert und weiter optimiert wurden. Für die Modellierung von resonanten Silizium-Drucksensoren sind daher verschiedene FE-Modelle entwickelt und der Einfluß der Geometrie- und der Materialeigenschaften unter verschiedenen Einspannbedingungen untersucht worden. Es wurden sowohl zweidimensionale FE-Modelle mit isotropen Materialeigenschaften, als auch dreidimensionale FE-Modelle unter der Berücksichtigung der vollen Materialanisotropie des Siliziums mit der 54,7° Randeinspannung infolge der (111)-Ebenen untersucht. Die maximale Abweichung der Resonanzfrequenzen zwischen der analytischen und der numerischen Beschreibung beträgt etwa 10 %. Der Unterschied zwischen isotropem und anisotropem Materialansatz bei Siliziummembranen führt zu einer Abweichung von etwa 3 % bei den Eigenfrequenzen der Grundbiege-Schwingungen. Eine weitere Erniedrigung der Resonanz-Frequenzen tritt infolge verminderter Einspannungssteifigkeit durch die schräge Randeinspannung ein, die in der gleichen Größenordnung liegt. Eine detaillierte Beschreibung der einzelnen Modelleinflüsse ist in [Sch 92] enthalten. In Bild 2.7 sieht man die an einem 2D-Modell berechneten Schwingungsmoden M_ij und die zugehörigen Frequenzvielfachen c_i = f_i / f_1 einer ebenen Silizium-Membran. Die Indizes i, j entsprechen der Anzahl der Schwingungsmaxima in der x- bzw. y-Richtung.
Bild 2.7: Numerisch ermittelte Eigenfrequenzen und Schwingungsmoden einer ebenen Silizium-Membran
Um die piezoelektrisch angesteuerten Drucksensormembranen experimentell zu charakterisieren, wurden sie optisch mit Hilfe eines Laser-Doppler-Vibrometers (POLYTEC OFV1102) vermessen. In Bild 2.8 ist das frequenz- und ortsabhängige Amplituden-Spektrum A(f,x) eines vom Verbundpartner Robert Bosch GmbH hergestellten Drucksensors abgebildet. Die Membranseitenlänge betrug 9,2 mm, die Siliziumdicke 50 μm und die ZnO-Schichtdicke etwa 15 μm. Die Resonanzamplitude der Grundmode M_11 lag bei etwa 1 μm. Die Schwingungsgüte betrug bei Normalluftdruck bei der Grundmode etwa 100, bei den Moden M_13 und M_33 etwa 310 bzw. 360. Ein Vergleich der experimentell und numerisch ermittelten lateralen Modenverläufe entlang der Membranmitte zeigt eine gute Übereinstimmung. Bei genügend großen Schwingungsamplituden (einige hundert nm) konnten alle experimentell ermittelten Moden mit Hilfe der FEM-Ergebnisse zugeordnet werden.
Bild 2.8: Frequenz- und ortsabhängiges Amplitudenspektrum A(f,x) eines piezoelektrisch angetriebenen Silizium-Drucksensors
Das Resonanzverhalten von druck-beaufschlagten Membranen wird von den in der Membran induzierten Membranspannungen beeinflußt, die bei “großen” Auslenkungen auftreten. Die nichtlinearen Effekten sind abhängig vom Verhältnis der Membrandicke zur Kantenlänge, des einwirkenden Druckes und der Einspannungsart [Fab 92a]. Für den Zusammenhang zwischen der Resonanzfrequenz f_0 einer unverspannten Membran und einer planaren Spannung σ in der Membran gilt [Bou 90]:
(Gleichung 5)
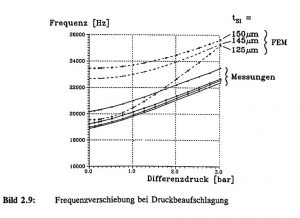
Diese Spannung kann durch äußere Lasten, z.B. Druckbeaufschlagung oder Temperaturbelastung oder durch prozeß-bedingte innere Spannungen hervorgerufen werden. In Bild 2.9 sind die Ergebnisse verschiedener FE-Berechnungen und optischer Messungen einer 148 μm dicken Silizium-Membran mit einer etwa 15 μm ZnO-Schicht dargestellt. Aufgrund der Resonanzfrequenz-Abweichung von etwa 4 kHz zwischen Messung und Simulation kann auf eine innere Druck-Spannung der ZnO-Schicht von etwa σ ≈ – 100 MPa unter Zugrundelegung von Gleichung (5) geschlossen werden. Der Einfluß der Schichtspannung bewirkt eine erhebliche Erniedrigung der Resonanzfrequenz der unbelasteten Membran gegenüber dem theoretischen Wert. Die gemessene Druck-Empfindlichkeit des Sensors beträgt in dem Meßbereich bis 3 bar etwa 1 Hz/mbar. Bei Erniedrigung der Membrandicke auf 125 μm konnte zwar der richtige Frequenzwert reproduziert werden, jedoch ist dies mit einer erhöhten Druckempfindlichkeit verbunden [Sch 92].
Bild 2.9: Frequenzverschiebung bei Druckbeaufschlagung
2.3 Piezoelektrische Anregung resonanter Sensoren
Für eine effiziente piezo-elektrische Anregung durch ZnO-Dünnschichten sind geeignet ausgelegte Elektrodenformen und das optimale Dickenverhältnis von ZnO-Schicht zur Dicke der Siliziumstruktur ausschlaggebend. Die Effizienz der Anregung läßt sich durch den effektiven elektro-mechanischen Kopplungsfaktor keff bestimmen. Dieser hängt im Gegensatz zum material-abhängigen Anteil k_mat, d.h. den mechanischen und elektrischen Eigenschaften der piezo-elektrischen ZnO-Schicht (Kapitel 2.1.2), von dem Schichtdicken-Verhältnis, der Bauteilgeometrie und den Randbedingungen ab. Es ist daher Ziel der piezo-elektrischen FE-Berechnungen unter Einschluß der Kopplung der mechanischen Größen (Verschiebungen) und der elektrischen Größen (Potential) die Sensor-Eigenschaften gezielt vorherzusagen und zu optimieren. Die Modellierung des piezo-elektrischen Effektes, der Wechselwirkung zwischen den räumlichen Verschiebungen und dem elektrischen Feld, erfolgt bei ANSYS durch eine Kopplung direkt auf der finiten Elementebene. Der implementierte Ansatz erlaubt es, das statische und dynamische Verhalten von linear piezoelektrischen Medien mit anisotropen Material-Eigenschaften zu untersuchen [AUM 92]. Es lassen sich mikromechanische Resonatoren modellieren, die durch piezo-elektrische Dünnschichten angeregt werden. Im Gegensatz zu einer mechanischen Anregung erfolgt diese direkt durch die elektrischen Feldgrößen, so daß unter Berücksichtigung der elektro-mechanischen Wandlung das mechanische Strukturverhalten berechnet und verschiedene elektrische Kenngrößen abgeleitet werden können.
2.3.1 Modellierung des elektrischen Sensorverhaltens
Die piezo-elektrisch angeregten Kraft- und Drucksensoren werden bei Applikation in einer Oszillatorschaltung betrieben, bei der das Impedanz- und Phasenverhalten (Zweipol-Betrieb) bzw. das elektrische Übertragungsverhalten (Vierpol-Betrieb) der Sensor-Elemente bekannt sein muß. Die Bestimmung des effektiven Kopplungsfaktors kann durch die Berechnung des frequenzabhängigen Impedanz- und Phasenverlaufes erfolgen. Für den effektiven Kopplungsfaktor k_eff einer Schwingungsmode eines piezo-elektrischen Resonators gilt [VIB 81]:
(Gleichung 6)
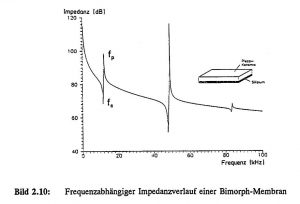
Unter Zugrundelegung des elektrischen Ersatzschaltbild für piezoelektrische Resonatoren [Tic 80], entspricht die Serien-Resonanzfrequenz f_s der elektrischen Kurzschluß-Bedingung (E=0) und die Parallel-Resonanzfrequenz f_p dem elektrischen Leerlauf bei offenen Elektroden (D=0). Zur Entwicklung geeigneter FE-Modelle und zur Verifikation der piezoelektrischen Berechnungsmöglichkeiten mit ANSYS wurde eine Bimorph-Struktur bestehend aus Silizium-Membran mit einer Piezokeramik (PZT) ausgewählt. Für die Piezokeramik liegen genaue Angaben zu Materialeigenschaften [VIB 81] vor, so daß der Einfluß von unbekannten Parametern auf ein Mindestmaß beschränkt werden konnte. Bei der Bimorph-Struktur betrug die Membranseitenlänge 9,2 mm, die Dicke der Silizium-Membran 20 μm und die Dicke der Piezokeramik 200 μm. Das Materialverhalten für die Piezokeramik (VIBRIT 420) wurde anisotrop modelliert. Die elektrische Anregungsspannung betrug an den ganz-flächigen Elektroden 1 V. Für die mechanische Schwingungsgüte Q wurde ein mittlerer Wert von 1000 angenommen, die dielektrischen Dämpfungsbeiträge wurden vernachlässigt.
In Bild 2.10 ist der mit FEM berechnete frequenzabhängige Impedanz-Verlauf der Bimorph-Membran bis 100 kHz in logarithmischer Darstellung aufgetragen. Drei Schwingungsmoden sind deutlich ausgeprägt, deren elektro-mechanischen Kopplungsfaktoren mit zunehmender Frequenz abnehmen (k_eff ≈ 29 %, 22 %, 16 %). Die mechanische Schwingungsamplitude der Grundmode wurde zu etwa 2,5 μm berechnet. Ein Vergleich der FE-Berechnungen mit Messungen zeigt trotz einfacher Modellansätze eine gute Übereinstimmung. Die Abweichungen bei den Resonanzfrequenzen betragen etwa 1-4 %.
Bild 2.10: Frequenzabhängiger Impedanzverlauf einer Bimorph-Membran
2.3.2 Optimierung des Schichtdickenverhältnisses
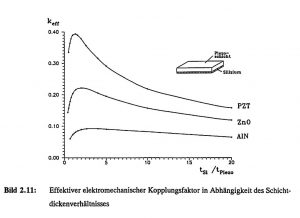
Bei der piezoelektrischen Anregung ist die Kenntnis des günstigsten Schichtdicken-Verhältnisses für eine möglichst hohe elektromechanische Kopplung von besonderem Interesse. Mit verschiedenen Bimorph-Modellen wurde der Einfluß des Schichtdicken-Verhältnisses der Piezoschicht t_Piezo zur Siliziummembran t_Si und die Auswirkung verschiedener piezoelektrischer Materialien untersucht. In Bild 2.11 ist der effektive elektromechanische Kopplungsfaktor für AlN, ZnO und PZT-Keramik in Abhängigkeit der Piezoschichtdicke für eine 20 μm dicke Silizium-Membran aufgetragen. Deutlich ist zu erkennen, daß die verschiedenen Materialien unterschiedliche optimale Schichtdicken aufweisen. Für AlN, ZnO und PZT werden die maximalen Kopplungsfaktoren von 10 %, 25 % und 39 % bei Schichtdicken von etwa 5-6 μm, 9 ± 1 μm und 15 ± 2 μm erreicht und liegen damit im realisierbaren Bereich der Dünnschichttechnik. Ein Vergleich mit experimentellen Werten und eine ausführliche Diskussion des Schichtspannungseinflusses beim Zinkoxid wird in Kapitel 4 gegeben.
Bild 2.11: Effektiver elektromechanischer Kopplungsfaktor in Abhängigkeit des Schichtdickenverhältnisses
2.3.3 Erhöhte Modenselektivität durch Elektrodenstrukturierung
Die Anregung resonanter Siliziumstrukturen zu Biege-Schwingungen erfolgt durch aufgesputterte ZnO-Dünnschichten, die infolge des piezoelektrischen Effektes, Dehnungen und Kontraktionen auf der Bauteiloberfläche erzeugen. Um eine möglichst hohe Modenselektivität zu erreichen, ist es wichtig den genauen Spannungsverlauf auf der Bauteiloberfläche zu kennen und durch eine geeignete Elektrodenformgebung sicherzustellen, daß im Bereich von Zugspannungen nur Dehnung, im Bereich von Druck-Spannungen nur Kontraktion erzeugt werden. Als Designparameter für die Elektroden-Auslegung ist der Nulldurchgang des lateralen Spannungsverlaufes (d.h. der Übergang von Zug- in Druck-Spannungsbereiche) auf der Oberfläche des Resonators anzusehen.
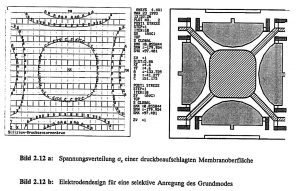
Ausgehend von einer Silizium-Membran wurden verschiedene FE-Modellen untersucht, wobei der Einfluß unterschiedlicher Membrandicken, variabler Druckbeaufschlagung, der Einspannung infolge der ätzbegrenzenden (111)-Ebenen und nichtlinearer Effekte, infolge Spannungsversteifung der Membran berücksichtigt wurden. Die FE-Berechnungen ergeben für den Nulldurchgang des lateralen Spannungsverlaufes einen Wert von etwa 17 % der Membranseitenlänge. Für beidseitig eingespannte Biegebalken beträgt der Nulldurchgang etwas weniger als 25 % der Balkenlänge. In diesen Bereichen sollten keine Elektroden angeordnet werden. In Bild 2.12 a ist die Spannungsverteilung σ_x auf einer von unten druck-beaufschlagten Membranoberfläche dargestellt. Im Randbereich bilden sich Druckspannungen, in Membranmitte Zugspannungen aus. Ein direkt aus der flächenhaften Spannungsverteilung abgeleitetes Elektrodendesign für eine selektive Anregung der Grundmode ist in Bild 2.12 b zu sehen.
Bild 2.12 a: Spannungsverteilung σ_x einer druck-beaufschlagten Membranoberfläche
Bild 2.12 b: Elektrodendesign für eine selektive Anregung des Grundmodes
Durch die Strukturierung der Elektroden und der gegenphasigen Ansteuerung zwischen Rand- und Zentralelektrode konnte die Modenselektivität der Grund-Mode deutlich erhöht und der Betrag der Resonanz-Amplitude bei gleicher Ansteuerung verdoppelt werden. Hierdurch kann der Sensor im Kleinsignalbereich betrieben und dynamische Nichtlinearitäten, hervorgerufen durch große Schwingungsamplituden, vermieden werden.
2.3.4 Vergleich der Berechnungen mit Messungen
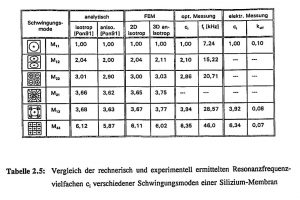
In Tabelle 2.5 werden die rechnerisch und experimentell ermittelten Resonanz-frequenzvielfachen c_i der Schwingungsmoden der Drucksensormembran miteinander verglichen. Die analytisch ermittelten Frequenz-vielfachen für isotropes und anisotropes Materialverhalten sind der Literatur [Pon 91] entnommen und gehen von Platten mit idealer Einspannung aus. Zum Vergleich wurden mit FEM sowohl 2D-Schalenmodelle mit isotropem Materialverhalten, als auch 3D-Volumenmodelle mit anisotropem Materialverhalten und (111)-Einspannung berechnet. Die Frequenzvielfachen der niedrigen Schwingungsmoden korrelieren gut mit den analytischen Ergebnissen, während die Abweichung zu höheren Schwingungsmoden hin zunimmt.
Im Vergleich zu den analytischen und numerischen Berechnungen fällt die gemessene Resonanzfrequenz der Grundmode einer ZnO-beschichteten Silizium-Membran um etwa 2 kHz geringer aus. Hieraus wurde die technologisch bedingte innere Druckspannung in der ZnO-Schicht nach Gleichung (5) zu σ ≈ -15 MPa abgeschätzt. Bei den elektrischen Messungen wurde mit Hilfe eines Impedance / Gain-Phase-Analyzers (HP4194A) das Impedanz- und Phasenverhalten der Drucksensor-Membranen vermessen und aus den Resonanzfrequenzen f_s und f_p der effektive Kopplungsfaktor k_eff bestimmt. Aufgrund der modenselektiven Elektrodenanordnung konnten nicht alle Moden elektrisch nachgewiesen werden, doch stimmen die Frequenzvielfachen für M_13 und M_33 sehr gut mit den optisch gemessenen Werten überein. Die Abweichung zu den berechneten Werten nimmt auch hier zu höheren Schwingungsmoden tendenziell zu [Fab 92b].
Tabelle 2.5: Vergleich der rechnerisch und experimentell ermittelten Resonanzfrequenzvielfachen c_ij verschiedener Schwingungsmoden einer Silizium-Membran
2.4 Zusammenfassung
Die Anforderungen beim Entwurf von resonanten Sensoren, sich überlagernde nichtlineare Effekte, anisotrope Materialeigenschaften und die piezo-elektrischen Wechselwirkungen bei Mehrschichtsystemen (Multilayer) zu berücksichtigen, bedingen den Einsatz rechner-gestützter, numerischer Berechnungsmethoden.
Eine Optimierung mikromechanischer Resonatoren kann nur unter gleichzeitiger Betrachtung der statischen und dynamischen Eigenschaften unter Einschluß des physikalischen Anregungsprinzips erreicht werden. Die durchgeführten Untersuchungen haben gezeigt, daß die Methode der Finiten Elemente (FEM) geeignet ist, das Verhalten mikromechanischer Sensoren zu beschreiben. Bei der Berechnung der Resonanzfrequenzen und Schwingungsmoden und der lastabhängigen Resonanzfrequenzänderung konnte eine gute Übereinstimmung mit den Meß-Ergebnissen erzielt werden.
Die Möglichkeiten des Programmsystems ANSYS, gekoppelte Feldberechnungen durchzuführen, erlauben eine Modellierung des Verhaltens piezoelektrisch angetriebener Sensoren. Damit ließen sich bereits in der Entwurfsphase wichtige Vorgaben, wie z.B. die günstigste Elektrodenanordnung und das optimale Schichtdicken-Verhältnis, für die nachfolgenden technologischen Prozeß-Schritte ableiten. Eine Stärke der FE-Methode ist es, komplexe Geometrien unter vielfältigen Randbedingungen modellieren, Parameterstudien durchführen und Geometrie- und Materialeinflüsse separat betrachten zu können.
Literaturverzeichnis
- [Ala 92] : Alavi, M., Fabula, Th., Schumacher, A., Wagner, H.-J., Monolithic Micro-bridges in Silicon Using Laser Machining and Anisotropic Etching”, EURO-SENSORS VI, San Sebastian (1992), erscheint in Sensors and Actuators
- [Alb 82] : Albert, W.C., Vibrating Quartz Crystal Beam Accelerometer, ISA 28th. Int. Instr. Symp., Vol.28, No.1 (1982)
- [AUM 92] : ANSYS User’s Manual for Revision 5.0, Volume IV, Theory, ed. Peter Kohnke, Houston, PA, USA (1992)
- [Ble 84] : Blevins, R.D., Formulas for natural frequency and mode shapes, Krieger Publishing Company, Malabar/Florida (1984)
- [Bou 90] : Bouwstra, S., Resonating microbridges mass flow sensor, Thesis, University of Twente, Enschede, The Netherlands (1990)
- [Bri 85] : Brice, J.C., Crystals for quartz resonators, Rev. Modern Physics, Vol. 57, No. 1 (1985) 105
- [Cha 87] : Chan, H.-L., Wise, K.D., Scaling limits in batchfabricated silicon pressure sensors, IEEE Transactions on Electronic Devices, Vol. ED-34, No.4, (1987), S. 850-858
- [Fab 92a] : Fabula, Th., Schroth, A., Simulation des dynamischen Verhaltens mikromechanischer Membranen, VDI-Fachtagung für Geräte- und Mikrosystemtechnik, TU Chemnitz (1992), VDI-Bericht 960, VDI-Verlag Düsseldorf (1992)
- [Fab 92b] : Fabula, Th., Dynamische Berechnungen in der Mikromechanik – Simulation / Messung, 10. ANSYS Users’ Meeting, Arolsen, 28.-30.10.1992
- [Fra 88] : Franz, J., Piezoelektrische Sensoren auf Siliziumbasis für akustische Anwendungen, VDI-Berichte, Reihe 10: Informatik/Kommunikationstechnik, Nr. 87, VDI-Verlag Düsseldorf (1988)
- [LB 82] : Landolt-Börnstein, Zahlenwerte und Funktionen aus Naturwissenschaft und Technik, Gruppe III, Band 17a, Berlin, Springer Verlag (1982)
- [Pon 91] : Pons, P., Blasquez, G., Natural vibration frequencies of silicon diaphragms, Proceedings: Transducers of the IEEE, San Francisco (1991)
- [SASI] : Swanson Analysis Systems Inc., Houston, PA, USA
- [Sch 92] : Schroth, A., Modellierung mikromechanischer Membranen, Diplomarbeit, TU Chemnitz / HSG-IMIT (1992)
- [Tic 80] : Tichy, J., Gautschi, G., Piezoelektrische Meßtechnik, Springer-Verlag, Berlin (1980)
- [Utt 87] : Uttamachandi, D., Thornton, K.E.B., Nixon, J., Culshaw, B., Optically excited resonant diaphragm pressure sensor, Electronics Letters, Vol.23, No.4, (1987), S. 152-153
- [VIB 81] : VIBRIT – Piezokeramik von Siemens, Datenblatt, Siemens AG, Redwitz, Stand: Januar 1981
- [You 50] : Young, D., Vibration of rectangular plates by the Ritz method, Journal of applied Mechanics, Dec.,(1950) S. 448-453
GitHub Repositories
- github.com/ThomasFabula/BMFT_FASENS
- github.com/ThomasFabula/Quartz-DETF
- github.com/ThomasFabula/piezoelectric_simulation
- github.com/ThomasFabula/Modeling-of-Resonant-Silicon-Microsensors
Weiterführende Informationen
Englische Version
Testimonials
Prof. Dr.rer.nat. Stephanus Büttgenbach | Technische Universität Braunschweig