Invited paper
“Sensors and Materials”
Special Issue : Resonant Microsensors
Paper
Analytical and finite element modeling of resonant silicon microsensors
- Authors: Thomas Fabula and Stephanus Büttgenbach
- Year of publication: 1997
- Volume: 9
- Number: 8
- Pagination: 501-519
Keywords
beam-on-diaphragm, pressure sensor, electromechanical coupling factor, finite-element modeling, modal analysis, mode coupling, piezoelectric thin films, resonant force sensors, resonant pressure sensors, stress stiffening, triple-beam force sensor, TBFT, triple-beam tuning fork
Abstract
“This paper is concerned with the modeling of resonant silicon microsensors using analytical as well as finite-element methods. In the case of simple resonator structures, ideal boundary conditions and isotropic material properties, analytical methods can be used to model the dynamic behaviour of resonant microsensors. For more complex resonator structures, arbitrary boundary conditions, anisotropic material properties, multi-layer structures, and in the presence of coupled-field effects, the finite-element method is well suited for simulating the behaviour of resonant microstructures. Beamlike force and diaphragm pressure sensors are used to demonstrate the capability of this method to calculate eigenfrequencies, mode shapes, load-dependent frequency changes and cross-sensitivities as well as to optimize the resonator geometry with respect to mode selectivity, mode decoupling, electromechanical coupling efficiency, and measuring range and sensitivity. The numerical results are compared to experimental data in order to verify the finite-element models.“
Introduction
Resonant sensors, which change their output frequency as a function of the quantity to be measured, are attractive because of their high sensitivity, high resolution, and semi-digital output. They are based on the fact that the frequency of acoustic waves in solids is a highly sensitive probe for parameters that alter the geometry or the boundary conditions of the resonating structure. This paper centres on silicon microsensors vibrating at their mechanical resonance frequency.(1-3) They are fabricated from single-crystal silicon using micromachining technologies like anisotropic wet etching and thin film deposition.(4)
For ideal boundary conditions the dynamic behaviour of simple resonator structures, for example double-clamped prismatic beams or all-around clamped flat diaphragms, may be modeled analytically with sufficient accuracy. In the case of arbitrary boundary conditions or of more complex resonator structures like non-prismatic beams, ‘butterfly’-resonators,(5) ‘H’-shaped resonators,(6) ‘beam-on-diaphragm‘-structures,(7-10) or triple-beam(11) and quadruple-beam(12) resonators it is very difficult or even impossible to perform the analysis on the basis of analytical models. Instead numerical methods like the finite element method(13) (FEM) may be used to study the behaviour of such resonators and to enable an efficient sensor design.
Principle of resonant silicon microsensors
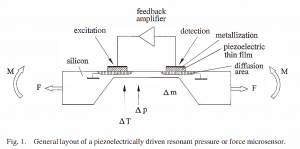
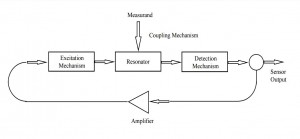
The general scheme of a resonant pressure or force microsensor, which is driven to resonant vibrations by piezoelectrical thin films, is shown in Fig. 1. The resonant element consists of a silicon diaphragm or beam wet etched from the backside of the wafer. Piezoelectric thin films, for example zincoxide (ZnO) layers,(14) are used to excite and to detect the vibrations of the resonator which is connected to the feedback loop of an oscillator circuit.
The fabrication process starts with the patterning and doping of the ground electrode areas. In order to achieve a high electromechanical coupling efficiency, ZnO has to be grown with its c-axis perpendicular to the film plane and the silicon substrate. Well-oriented ZnO films may be deposited by r. f. sputtering from a Zn or ZnO target in an Ar/O2 plasma. The ZnO is wet etched in a stirred solution of HAc, H3PO4, and H2O in order to form the piezoelectrically active regions. A sputtered and patterned Al metallization layer is used as the top electrode contact for the ZnO film. After completing the planar front-side process, anisotropic wet etching from the rear is applied to produce the desired beam or diaphragm thickness. In the case of beamlike resonators, in the final step deep trenching is performed by plasma etching the diaphragm from the front side.
Mechanical loading of the resonator due to a pressure difference Δp at the diaphragm or due to external forces F and moments M exerted on the beam results in a tensile stress in the resonator element. Stress stiffening effects will occur, which increase the stiffness of the resonator, thus changing its resonance frequency. Furthermore, a mass loading Δm or a temperature rise ΔT may lead to a frequency decrease. The output of the electronic oscillator circuit is fed to a frequency counter recording the load-dependent signal. The resonant microsensors considered in the following study are based on this principle; they consist of the passive resonator element (i.e. beam, membrane, etc.) and active elements for excitation and detection (electronics) of vibrations.
Analytical description
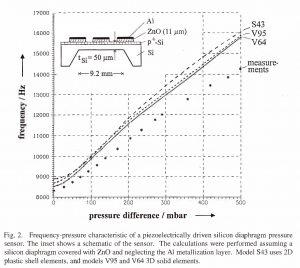
Using methods like modal analysis or Laplace transforms(15) the dynamic behaviour of double-clamped beams and all-around clamped flat diaphragms may be calculated analytically. Assuming homogeneous and isotropic material properties, the resonance frequencies, mode shapes, and load-dependent frequency changes can be calculated with sufficient accuracy.
For a doubly clamped beam the force-dependent frequency of then-th natural mode … may be approximated for the free, undamped case by:
Limitations of analytical methods
Analytical solutions to the boundary-value problems involving the static and dynamic behavior of resonant microsensors can be obtained only in special cases by assuming several idealizations as described above. The main disadvantage is that the exact boundary conditions cannot be accounted for, especially if the stiffnesses of the resonator and the clamping region are of the same order of magnitude. Furthermore, nonhomogeneous and anisotropic material properties as well as structured multilayer systems and distributed loads cannot be modeled.
The Finite-Element Method
As a general numerical approximation method, finite-element modeling facilitates the calculation of complex micromechanical resonators with arbitrary boundary conditions under the influence of nonlinear mechanisms. In addition, coupled-field effects such as electromechanical coupling can be accounted for. In the following we give an outline of the mathematical basis and program implementation. In section 5 the capabilities of this method are demonstrated with the help of several examples.
Numerical Modeling
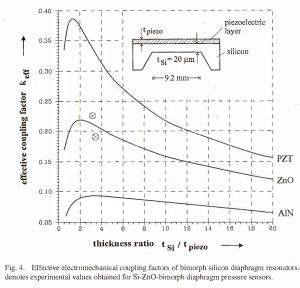
The time required for the design and fabrication processes of rnicrosensor devices can be considerably reduced by utilizing computer simulations. In addition, modeling provides a unique insight into the mode of operation of the devices. Numerical methods such as FEM are powerful tools for modeling the dynamic response of resonant sensors and for predicting the performance of microsensors under operating conditions. Geometry related effects, in particular, can be studied, for example, the optimization of clamping and decoupling regions, the calculation of the influence of various resonator cross-sectional shapes, and the estimation of mode shapes of complex resonator structures. Furthermore, FEM is a valuable tool for the development of multilayer structures such as piezoelectrically driven microsensors and actuators.
Conclusion
For the optimization of the performance of resonant silicon microsensors a profound insight into their internal behaviour is necessary. To achieve this in a reasonable time, modeling and numerical simulation are necessary. For simple resonator structures with ideal boundary conditions analytical models may be used to calculate their characteristics with sufficient accuracy if homogeneous and isotropic material behaviour is assumed.
For more complex resonator structures, arbitrary boundary conditions, anisotropic and temperature-dependent material properties, and in the presence of coupled-field effects FEM can be used to simulate the properties of resonant microstructures. Beam-like force and diaphragm pressure sensors have been used to demonstrate the capability of this method to calculate eigenfrequencies, mode shapes, load-dependent frequency changes and cross-sensitivities as well as to optimize the resonator geometry with respect to mode selectivity, mode decoupling, electromechanical coupling efficiency, measuring range, and sensitivity.
 These examples clearly demonstrate that finite element modeling is an indispensable tool for the development of complex resonant microstructures as well as for the development of active multilayer structures used to excite the vibrations. For these purposes several finite element codes are commercially available, and different computer platforms may be used to perform such analyses.
These examples clearly demonstrate that finite element modeling is an indispensable tool for the development of complex resonant microstructures as well as for the development of active multilayer structures used to excite the vibrations. For these purposes several finite element codes are commercially available, and different computer platforms may be used to perform such analyses.
Acknowledgements
This work was partially supported by the Bundesministerium für Forschung und Technologie (today: BMBF) under contract number 13 AS 0114.
References
- Stemme: Resonant silicon sensors, J. Micromech. Microeng. 1 (1991) 113-125
- H.A.C. Tilmans, M. Elwenspoek, J.H.J. Fluitman: Micro resonant force gauges, Sensors and Actuators A30 (1992) 35-53
- R.A. Buser: Resonant Sensors, in: Sensors, Vol. 7, Mechanical Sensors, ed. H.H. Bau, N.F. de Rooij, B. Kloeck (VCH, Weinheim, 1994) pp. 205-284
- S. Büttgenbach: Mikromechanik (Teubner, Stuttgart, 1991)
- J.C. Greenwood, D.W. Satchell: Miniature silicon resonant pressure sensor, IEE Proceedings 135 (1988) 369-372
- K. Ikeda, H. Kuwayama, T. Kobayashi, T. Watanabe, T. Nishikawa, T. Yoshida, K. Harada: Silicon pressure sensor integrates resonant strain gauge on diaphragm, Sensors and Actuators A21-A23 (1990) 146-150
- K.E.B. Thornton, D. Uttamchandani, B. Culshaw: A sensitive optically excited resonator pressure sensor, Sensors and Actuators A24 (1990) 15-19
- R.A. Buser, L. Schultheis, N.F. de Rooij: Silicon pressure sensor based on a resonating element, Sensors and Actuators A25-27 (1991) 717-722
- K. Petersen, F. Pourahmadi, J. Brown, P. Parsons, M. Skinner and J. Tudor: Resonant silicon beam pressure sensor fabricated with silicon fusion bonding, Proc. 6th Int. Conf. Solid-State Sensors and Actuators (Transducers ’91), San Francisco, 1991, pp. 664-667
- A. Schumacher, M. Alavi, Th. Fabula, B. Schmidt, H.-J. Wagner: Monolithic bridge-on-diaphragm microstructure for sensor applications, Proc. Micro System Technologies 94, Berlin, 1994
- Th. Fabula, H.-J. Wagner, B. Schmidt, S. Büttgenbach: Triple-beam resonant silicon force sensor based on piezoelectric thin films, Sensors and Actuators A41-42 (1994) 375-380
- H.A.C. Tilmans: Micro-mechanical encapsulated built-in resonant strain gauges, Ph.D. thesis (University of Twente, Enschede, 1993)
- K.J. Bathe: Finite element procedures in engineering analysis (Prentice Hall Inc., Englewood Cliffs, 1982)
- J.G. Smits, H.A.C. Tilmans, K. Hoen, H. Mulder, J. van Vuuren, G. Boom: Resonant diaphagm pressure measurement system with ZnO on Si excitation, Sensors and Actuators 4 (1983) 565-571
- A. Prak: Silicon resonant sensors: operation und response, Ph.D. thesis (University of Twente, Enschede, 1993)
- W. Weaver, S.P. Timoshenko, D.H. Young: Vibration problems in engineering (John Wiley & Sons, New York, 1990)
- S. Bouwstra, B. Geijselaers: On the resonance frequencies of microbridges, Proc. 6th Int. Conf. Solid-State Sensors and Actuators (Transducers `91), San Francisco, 1991, pp. 538-542
- S.P. Timoshenko, S. Woinowsky-Krieger: Theory of plates and shells (McGraw-Hill Book Co., New York, 1987)
- D. Young: Vibration of rectangular plates by the Ritz method, J. Appl. Mech., Dec. (1950) 448-453
- R.D. Blevins: Formulas for natural frequency and mode shapes (Krieger Publishing Company, Malabar, 1984)
- P. Pons, G. Blasquez: Natural vibration frequencies of silicon diaphragms, Proc. 6th Int. Conf. Solid-State Sensors and Actuators (Transducers `91), San Francisco, 1991, pp. 543-546
- D. Uttamchandani, K.E.B. Thornton, J. Nixon, B. Culshaw: Optically excited resonant diaphragm pressure sensor, Electron. Lett. 23 (1987) 152-153
- Th. Fabula, A. Schroth: Simulation des dynamischen Verhaltens mikromechanischer Membranen, VDI-Berichte 960 (VDI, Düsseldorf, 1992)
- H.L. Chau, K.D. Wise: Scaling limits in batch-fabricated silicon pressure sensors, IEEE Trans. Electron Devices ED-34 (1987) 850-858
- D. Braess: Finite Elemente (Springer, Berlin, 1991)
- P.G. Ciarlet: The finite element method for elliptical problems (North-Holland, Amsterdam, 1978)
- A. Matzenmiller, W. Rust: ANSYS-Seminar Notes: Nonlinearities (CADFEM GmbH, Grafing, 1993)
- P. Kohnke (ed.): ANSYS User’s Manual for Revision 5.0, Volume IV, Theory (Swanson Analysis Systems, Inc., Houston, 1992)
- C.C. Rankin, F.A. Brogan: An element independent corotational procedure for the treatment of large rotations, J. Pressure Vessel Techn. 108 (1986) 165-174
- H. Allik, T.J.R. Hughes: Finite element method for piezoelectric vibration, Int. J. Numerical Methods in Engineering 2 (1970) 151-157
- L.D. Clayton, S.R. Swanson, E.P. EerNisse: Modifications of the double-ended tuning fork geometry for reduced coupling to its surroundings: finite element analysis and experiments, IEEE Trans. Ultrasonics, Ferroelect., Freq. Control UFFC-34 (1987) 243-252
- S.P. Beeby, M.J. Tudor: Modelling and optimisation of micromachined silicon resonators, Techn. Digest, Micromechanics Europe ’94, Pisa, Italy, 1994, pp. 44-47
- M. Alavi, Th. Fabula, A. Schumacher, H.-J. Wagner: Monolithic microbridges in silicon using laser machining and anisotropic etching, Sensors and Actuators A37-38 (1993) 661-665
- Swanson Analysis Systems, Inc., Houston, USA
- Landolt-Börnstein: Zahlenwerte und Funktionen aus Naturwissenschaft und Technik, Gruppe III, Band 17a (Springer, Berlin, 1982)
- G.J. Tijhuis: Onderzoek naar het druk-frequentie verband van een resonerende membraan druksensor, Diploma thesis (University of Twente, Enschede, 1987)
- Th. Fabula: Dynamische Berechnungen in der Mikromechanik – Simulation / Messung, Proc. 10. ANSYS Users´ Meeting, Arolsen (CADFEM GmbH, Grafing, 1992)
- H.J.M. Geijselaers, H. Tijdeman: The dynamic mechanical characteristics of a resonating microbridge mass-flow sensor, Sensors and Actuators A29 (1991) 37-41
- Th. Fabula, N. Hey, S. Messner: Gekoppelte Feldberechnung eines mikromechanischen Strömungssensors, Proc. 11. CADFEM Users’ Meeting, Bamberg (CADFEM GmbH, Grafing, 1993)
- Th. Fabula: Dynamisches Verhalten mikromechanischer Strukturen – Finite Elemente Simulation zur Entwurfsunterstützung und deren meßtechnische Verifikation, Ph.D. thesis (University of Bonn, 1994)
- R. Lerch: Simulation of piezoelectric devices by two- and three-dimensional finite elements, IEEE Trans. Ultrasonics, Ferroelect., Freq. Control UFFC-37 (1990) 233-247
- G. Flik (Robert Bosch GmbH): private communication
- SDRC: Structural Dynamics Research Corporation, Milford, USA
Journal
Sensors and Materials, MYU Tokyo : www.myu-inc.jp/myukk/S&M
Further Links
GitHub repositories
- github.com/ThomasFabula/Modeling-of-Resonant-Silicon-Microsensors
- github.com/ThomasFabula/piezoelectric_simulation
- github.com/ThomasFabula/ANSYS_MEMS