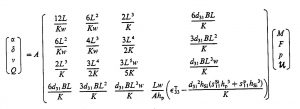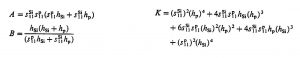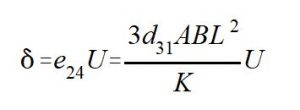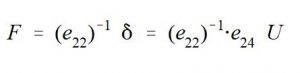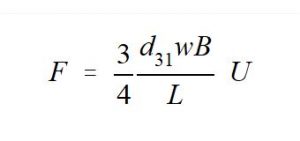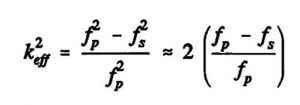Antrieb von Aktoren durch piezoelektrische Dünnschichten
Dipl.-Phys. Th. Fabula
Hahn-Schickard-Gesellschaft für Angewandte Forschung e.V.
Februar 1993
Piezoelektrische Dünnschicht-Materialien
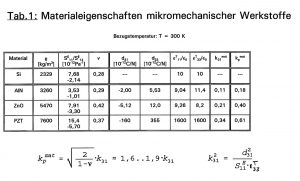
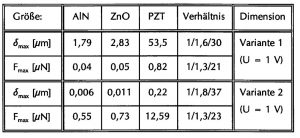
Für die Abschätzung der Leistungsfähigkeit des piezoelektrischen Antriebs werden die Materialien Aluminiumnitrid (AlN), Zinkoxid (ZnO) und PZT-Keramiken (PZT) zugrunde gelegt, die auch als Dünnschichten hergestellt werden können. Da die Materialdaten stark von der Art des Herstellungsprozesses und der Prozeß-Parameter abhängig sind, fehlen für dünne Schichten meist genaue Materialangaben. Für die folgenden Abschätzungen beziehen sich die Materialdaten, soweit nicht anders angegeben auf Bulk-Material ([Fra88], [Lan82], [Sie81]). Hinzu kommt, daß die Material-eigenschaften schichtdickenabhängig und die abgeschiedenen Schichten innere mechanische Spannungen aufweisen. In der Literatur schwanken die Angaben beispielsweise für ZnO im Vergleich zu den Bulk-Daten bei den Elastizitätsmodulen um ca. ± 20%, die Schichtspannungen bewegen sich im Bereich bis einige hundert MPa (Zug- und Druckspannung), die Abweichung bei den Dielektrizitätskonstanten (Permittivitäten) beträgt Δεr ≈ 10%, die piezo-elektrischen Koeffizienten d_ij variieren um etwa +/- 15-20%.
Piezoelektrische Kopplungsfaktoren
Ein Maß für die Effizienz des piezoelektrischen Antriebs ist der elektromechanische Kopplungsfaktor k. Er erlaubt eine Aussage über die Möglichkeit der Umwandlung von mechanische E_mech in elektrische Energie E_elek eines Materials: k2 = E_mech / E_elek. Dieser Kopplungsfaktor ist sowohl von den Materialeigenschaften, als auch von der Geometrie des Wandlers abhängig, sodaß sich ein effektiver elektromechanischer Kopplungsfaktor keff = k_mat ⋅ k_geo ergibt.
Tabelle 1 zeigt einen Vergleich der Materialeigenschaften verschiedener Piezoelektrika und erlaubt eine Abschätzung der theoretisch zu erwartenden materialabhängigen elektromechanischen Kopplungsfaktoren kmat. Aufgeführt sind die beiden Kopplungsfaktoren k31 bzw. kp für einen reinen Transversal- bzw. Planarwandler [VIB]. In Abhängigkeit der unterschiedlichen mechanischen Steifigkeiten (E-Modul: E = 1 / S11), der piezo- und dielektrischen Eigenschaften ergeben sich für Aluminiumnitrid, Zinkoxid bzw. PZT-Keramik (VIBRIT420, siehe technischen Datenblatt VIBRIT®, Piezoelectric Ceramics from Siemens, Data Sheet, Edition 1981) unterschiedlich große Kopplungsfaktoren in der Größenordnung von etwa 18%, 40% und 60%. Ein Vergleich der beiden Kopplungsfaktoren k31 und kp zeigt, daß der Unterschied bis zu einem Faktor 2 betragen kann. Betrachtet man zusätzlich die Schwankungen der einzelnen Materialdaten bei ZnO wie oben angegeben, so kann die Gesamtabweichung (Δk31/k31)² = (Δd31/d31)² + (ΔS11/2S11)² + (Δεr/2ε)² ≈ 25% betragen, d.h. k31 = 0,21 + 25%. Dies führt auf einen erhöhten Kopplungsfaktor von k_pmat ≈ 50%. Der Einfluß der Aktorgeometrie auf den Kopplungsfaktor (d.h. k_geo) kann mit Hilfe numerischer Finite-Elemente Berechnungen unter Berücksichtigung der mechanischen und elektrischen Randbedingungen ermittelt werden.
Analytische Abschätzungen der erreichbaren Hübe und Kräfte
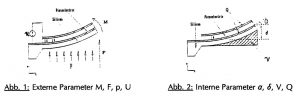
Bei der analytischen Abschätzung soll von einem einseitig eingespannten Silizium-Biegebalken ausgegangen werden, der von einer piezoelektrischen Dünnschicht bedeckt ist. In der Literatur (siehe [Smi91a], [Smi91b]) ist der Zusammenhang zwischen den externen Parametern (Drehmoment: M, Kraft: F, Druck: p und Spannung: U, siehe Abb. 1) und den internen Parametern (Ablenkungswinkel: α, Auslenkung: δ, Verschiebungsvolumen: V und Ladung: Q, siehe Abb. 2) aus den piezoelektrischen Zustandsgleichungen abgeleitet.
Abb. 1: Externe Parameter M, F, p, U
Abb. 2: Interne Parameter α, δ, V, Q
Die symmetrische Übertragungsmatrix e_ij beschreibt den Biegezustand des Balkens bei unterschiedlichen mechanischen und elektrischen Belastungen:
Die vollständigen Beziehungen lauten:
mit den Abkürzungen A, B, K:
wobei:
- L, w : Länge, Breite des Biegebalkens [m]
- hSi : Substratdicke (hier Silizium) [m]
- hp : Dicke der Piezoschicht [m]
- SSi11 : Steifigkeitskoeffizient des Substrats [m2/N]
- Sp11 : Steifigkeitskoeffizient der Piezoschicht [m2/N]
- d31 : transversaler piezoelektrischer Koeffizient [C/N]
- ε33 : Dielektrizitätskonstante in E-Feldrichtung [As/Vm]
Die maximale Auslenkung δ beträgt am Balkenende bei Anlegen einer Spannung U an die piezoelektrische Schicht:
Die maximal erreichbare Kraft, die der Bimorph-Balken ausüben kann, läßt sich durch die Federsteifigkeit e22-1 ausdrücken:
Der vollständige Zusammenhang ergibt sich zu:
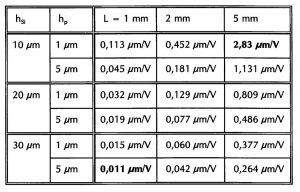
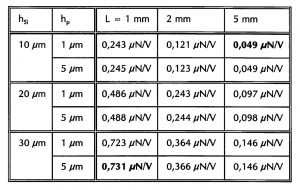
In den obigen Ausdrücken gewichten die Konstanten A [m/Pa3], B [mPa] und K [m4/Pa2] die Steifigkeiten mit den entsprechenden Schichtdicken. Der Zusammenhang zwischen der Auslenkung δ bzw. ausübbaren Kraft F und der angelegten elektrischen Spannung U ist linear. Die Abhängigkeit von der Balkenlänge L ist bei der Auslenkung quadratisch, bei der Kraft umgekehrt proportional. Nachfolgend soll der Einfluß der Wandlergeometrie untersucht werden. Variiert wurden die Balkenlänge L, die Substratdicke h_Si und die Piezoschichtdicke h_p. Die Steifigkeitskoeffizienten vom Silizium-Substrat SSi11 und der Piezoschicht Sp11, sowie der transversale piezoelektrische Koeffizient d_31 für ZnO wurden der Tabelle 1 entnommen. Tabelle 2 enthält die Proportionalitätskonstanten e_24 zwischen der Auslenkung und der angelegten Spannung U. Die Balkenbreite w beträgt bei den Abschätzungen 50 μm:
Tabelle 2: Auslenkungs-Konstanten e24 für einen Silizium-Balken mit ZnO-Schicht
Tabelle 3: Kraft-Konstanten e24/e22 für einen Silizium-Balken mit ZnO-Schicht
Tabelle 4: Einfluß des Schichtsystems auf die Auslenkungen und Kräfte
FEM-Berechnungen
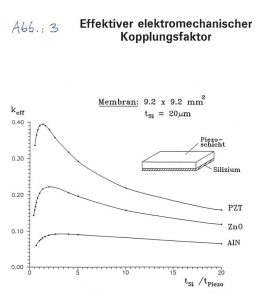
Effektiver elektro-mechanischer Kopplungsfaktor
Optimierung des piezoelektrischen Antriebs
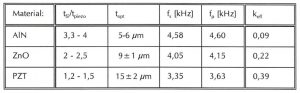
Tabelle 5: Vergleich der Materialien AlN, ZnO und PZT. Abhängigkeit des effektiven Kopplungsfaktors k_eff vom Schichtdickenverhältnis
GitHub repositories
- github.com/ThomasFabula/Modeling-of-Resonant-Silicon-Microsensors
- github.com/ThomasFabula/piezoelectric_simulation
- github.com/ThomasFabula/ANSYS_MEMS
Literaturverzeichnis
- [Fra88] : Franz, J.: Piezoelektrische Sensoren auf Siliziumbasis für akustische Anwendungen, Fortschritt-Berichte VDI, Reihe 10, Nr.: 87, VDI Verlag, Düsseldorf (1988)
- [Lan82] : Landolt-Börnstein, Zahlenwerte und Funktionen aus Naturwissenschaft und Technik, Gruppe III, Band 17a, Berlin, Springer Verlag (1982)
- [Sie81] : VIBRIT – Piezokeramik von Siemens, Datenblatt, Stand: Januar 1981, Redwitz
- [Smi91a] : Smits, J.G., Dalke, S.I., Cooney, T.K., The constituent equations of piezoelectric bimorphs, Sensors & Actuators A, 28 (1991) p. 41-61
- [Smi91b] : Smits, J.G., Choi, W., The constituent equations of piezoelectric heterogeneous bimorphs, IEEE Transactions on UFFC, Vol. 38, No. 3 (1991), p.256
- [Smi92a] : Smits, J.G., Choi, W., Very large deflection with quadratic voltage dependence of ZnO on Si3N4 bimorph, IEEE Transactions on UFFC, Letters, Vol. 39, No. 2 (1992) p. 302
- [Smi92b] : Smits, J.G., Design consideration of a piezoelectric-on-silicon microrobot, Sensors & Actuators A, 35 (1992) p. 129-135
- [VIB] : VIBRIT® – Piezoceramics from Siemens, Ord.-No.: N-281/5035-101