Resonante Silizium-Sensoren

mit elektrothermischer Anregung und DMS in Metall-Dünnfilm-Technolgie

 

H. Bartuch*, S. Büttgenbach**, Th. Fabula***, H. Weiss*

 

* Gesellschaft für Mikrotechnik und Sensorik mbH, Richthofenstraße 3, D-78048 VS-Villingen
** Institut für Mikrotechnik der Technischen Universität Braunschweig, Langer Kamp 8, D-38106 Braunschweig
*** Institut für Mikro- und Informationstechnik der Hahn-Schickard-Gesellschaft für angewandte Forschung e.V., Wilhelm-Schickard-Straße 10, D-78052 Villingen-Schwenningen

 

Vortrag

Eingereicht als Vortrag anläßlich der SENSOR 93 in Nürnberg, vom 12.-14. Oktober 1993

 

Abstract

There is considerable interest in sensors based on mechanical resonance due to their high sensitivity to physical and chemical parameters and their frequency output. This paper reports on a study of electrothermally driven resonant silicon beams fabricated by micromachining and standard thin film technologies. The vibration of the beams is detected by metal strain gauges. The force as well as the gas flow sensitivity of the resonance frequency have been measured. The results show a fundamental resonance frequency of 4.265 kHz for a beam of 10 mm length, 1 mm width and 50 μm thick­ness, and frequency shifts of about 170 Hz/N (F = 1-10 N) and 100 Hz/m/s (v = 1-3 m/s), respectively. There is satisfactory agreement with results obtained from finite element modeling.

 

Einleitung

Moderne Meß‑ und Regelsysteme sind infolge der raschen Entwicklung der Mikroelektronik in zunehmendem Maße digi­tale Systeme. Für solche Systeme benötigt man Sensoren, die hinsichtlich ihrer Leistungsfähigkeit und ihrer geometrischen Abmessungen der Mikroelektronik angepaßt sind und mit dieser räumlich in einer Funk­tions­einheit integriert werden können. Zu ihrer Herstellung bietet sich als Miniaturisierungstechnologie die Mikromechanik an.

Neben konventionellen Sensoren mit Analog‑Digital‑Wandlern spielen Sensoren mit Frequenzausgang eine große Rolle. Eine wichtige Möglichkeit zur Erzeugung eines frequenzanalogen Sensorsignals bieten mecha­nische schwingungsfähige Strukturen, deren Resonanzfrequenz durch Änderung des mechanischen Span­nungs­zustandes von der zu messenden Größe abhängt. Als Werkstoff für mikromechanische Resonatoren ist ein­kristal­liner Quarz von großer Bedeutung, da er als nicht-zentrosymmetrischer Kristall piezoelektrisch ist. Aufgrund der hochentwickelten Verfahrenstechnik der Siliziumtechnologie und der hervorragenden mecha­ni­schen Eigenschaften ist auch Silizium ein wichtiger Werkstoff für mikro­mecha­ni­sche Resonatoren [Duf 92]. Da es nicht piezoelektrisch ist, muß zur Anregung entweder eine piezo­elek­trische Schicht aufgebracht werden oder Anregung und Abtastung der Schwingungen müssen auf andere Weise erfolgen. Dabei stellt die elek­tro-thermische Anregung eine relativ einfach zu realisierende Möglichkeit des Antriebes dar [Bou 90].

Die nachfolgend dargestellten Ergebnisse zeigen, daß das Prinzip der elektrothermischen Anregung und der resistiven Abtastung mittels auf dem Balken applizierter DMS (Abb. 1) auch für vergleichsweise massereiche Silizium­-Resonatoren anwend­bar ist. Der Einfluß mechanischer Vorspannungen auf die experi­mentellen Ergebnisse wird im Zusammenhang mit analytischen Rechnungen und Finite-Elemente‑Modellierungen (FEM) diskutiert.

 

Abb. 1:  Prinzip des elektrothermischen Antriebes

 

Design und Herstellung der Sensoren

Design

Die Grundstruktur der Sensoren (Abb. 2) besteht aus einem 50 μm dicken und 1 mm breiten Silizumbalken als Biege­schwinger, der von einem etwa 380 μm dicken und damit vergleichsweise starren Silizium‑Rahmen um­geben ist. Die Balkenlängen betragen 8 bzw. 10 mm. Diese Geometrie kann im FE-Modell durch einen beidseitig fest einge­spannten Balken mit trapezförmigem Querschnitt angenähert werden.

An den Balkenenden sind die zur thermischen Anregung notwendigen Mikroheizwiderstände (300 Ω) platziert, während die DMS‑Widerstände (200 Ω) in Balkenmitte bzw. in Nähe der Balkenenden so angeordnet sind, daß eine mög­lichst große Brückenverstimmung erreicht wird. Um eine Außenkontaktierung zu ermöglichen bzw. um ver­schie­dene Meß­größen einleiten zu können wurden die Chips auf Keramikzwischenträger geklebt.

 

Schichtaufbau

(100)‑Si‑Wafer mit:

• 1,2 μm thermischem Oxid
• 30 nm NiCr‑Widerstandsschicht
• 320 nm Ti/Au‑Kontaktschicht
• 3 μm Au (galv.)‑Bondschicht oder
• 450 nm Ti/Pd/Au-Lötkontaktschicht.

 

Mit diesem Schichtsystem sind, wie entsprechende Untersuchungen zum elektrischen Alterungsverhalten gezeigt haben, obere Einsatztemperaturen von 150°C für den Sensor realistisch. Die Widerstandsänderungen und damit die Änderung der elektrischen Leistungsaufnahme belaufen sich bei dieser Temperatur über einen Zeitraum von 1000 h auf einige Promille.

 

 

Abb. 2:  Geometrie und elektrisches Layout der Sensoren (schematisch)

 

 

Technologieabfolge

Die Umsetzung des elektrischen Layouts einschließlich der bond‑ bzw. lötbaren Außenanschlüsse erfolgte durch­­gängig in Metalldünnfilmtechnologie. Die hochstabilen NiCr‑Schichten wurden partiell reaktiv gesputtert.  Die Abscheidung des Kontaktschichtsystems erfolgte mittels Elektronenstrahlverdampfen. Zur Strukturierung  wurden übliche photo­litho­graphische und naßchemische Prozeßschritte angewandt.

Wie dem vereinfachten Technologieablaufschema in Abb. 3 zu entnehmen ist, ergibt sich eine gute Kompatibilität dieser Verfahrensschritte mit der Silizium‑Ätztechnologie zur Herstellung der Balkenstrukturen. Zur Reali­sie­rung der Vorder‑ zur Rückseitenpositionierung und zur Ausrichtung des Gesamtlayouts bezüglich des Silizium‑Kristallgitters erwiesen sich Laserjustierbohrungen als geeignet.

 

 

Abb. 3:  Vereinfachtes Technologieablaufschema zur Herstellung der Sensoren

 

 

Experimentelle Untersuchungen und Diskussion der Ergebnisse

Schwingungsverhalten

 

Fremdanregung

Um das dynamische Verhalten der Balkenresonatoren ohne Temperatureinfluß zu unter­suchen, wurden sie ohne Metall­schicht­system mit Hilfe von Piezokeramiken über Körperschall zum Schwingen angeregt. Die Abtastung erfolgte interferometrisch mit einem Laser-Vibrometer (POLYTEC OFW1102), unter Verwendung der Laser-Doppler­technik, so daß Biegeschwingungen aus der Balkenebene heraus detektiert werden können.

In Tab. 1 sind die gemessenen Resonanzfrequenzen im Vergleich mit FEM-Berechnungen zusammengestellt [Bra 92]. Die Model­­lierung erfolgte drei­dimen­sional mit isotropen Materialkennwerten unter Berücksichtigung der schrägen Balkeneinspannung durch die (111)-Siliziumebenen. Die ersten beiden Oberschwingungen aus der Balken­ebene heraus sind mit Z2 und Z3 gekenn­zeichnet und besitzen zwei bzw. drei Schwingungsbäuche. Die Abwei­chun­gen zu den gemessenen Werten betragen etwa 5-6 % infolge der durch die SiO₂-Schicht bewirkte innere Vorspannung [Mur 92].

 

Mode	FEM-Berechnung		Messung
	L = 10 mm	L = 8 mm	L = 10 mm	L = 8 mm
Z1	4,349 kHz	6,787 kHz	4,150 kHz	7,255 kHz
Z2	12,010 kHz	18,760 kHz	11,390 kHz	19,445 kHz
Z3	23,612 kHz	36,941 kHz	22,410 kHz	36,435 kHz

 

Tab. 1:  Resonanzfrequenzen von Silizium-Biegebalken bei Fremdanregung im Vergleich mit FEM-Berechnungen

 

Die Resonanzfrequenz der Grundbiegeschwingung eines doppelseitig eingespannten Biegebalkens der Länge L und Dicke t läßt sich analytisch berechnen:

 

Bei den Biegeschwingungen erfolgt die Balkendehnung in <110>-Kri­stall­richtung, so daß für den Elasti­zi­täts­modul E = 168,9 GPa und für die Poissonzahl v = 0,063 verwendet wurde. Die Dichte ρ von Silizium beträgt 2329 kg/m³. Die angegebenen Material­daten beziehen sich auf Zimmer­temperatur. Die analytische Berechnung nach Gleichung (1) ergibt für unverspannte Siliziumbalken bei 10 bzw. 8 mm Resonatorlänge Resonanz­fre­quenzen von 4,386 kHz bzw. 6,853 kHz in guter Übereinstimmung (1%) mit den numerisch berechneten Ergebnissen.

 

 

Elektrothermischer Antrieb

Durch Ansteuerung der Mikroheizer mit Impulsen geeigneter Folgefrequenz und ausreichender elektrischer Leistung werden die Siliziumbalken in Resonanz versetzt [Wie 93]. Für mittlere Heizleistungen von etwa 50 mW und ohne Anlegen einer Brückenspeisespannung (d.h. Niedertemperaturbereich) stimmen die durch optische Abtastung ermittelten Reso­nanz­­frequenzen gut mit denen der Fremdanregung überein. Da die Eigenerwärmung der Sensoren in diesem Fall sehr gering ist (ΔT zur Um­ge­bung < 4 K) kann daraus gefolgert werden, daß das auf dem Balken befindliche Metall­schichtsystem gegen­über der SiO₂‑Schicht keine wesentlichen Veränderungen der mecha­ni­schen Vorspannungen der Balken hervorruft. Für die aufgenommenen Amplitudenspektren ist charak­teristisch, daß aufgrund der symmetrischen Anregung als Schwin­gungs­moden nur die Grundmode (Z1) und die zweite Obermode (Z3) vorkommen.

In Abb. 4 sind die experimentell ermittelten Eigenschwingungsformen eines 10 mm langen Balkens im Ver­gleich mit FEM‑Berechnungen dargestellt. Der Balken wurde elektrothermisch mit einer niedrigen Heizleistung von P_Heiz = 50 mW ange­regt und optisch abgetastet [Mül 92]. Die relativen Schwingungsamplituden der rechnerischen Modalanalyse wurden auf die gemessenen Maximalwerte normiert.

 

• Z1-Mode: f₁ = 4,23 kHz
• Z3-Mode: f₃ = 24,1 kHz

 

Abb. 4 :  Experimentell ermittelte Eigenschwingungsformen des Biegebalkens im Vergleich mit FEM-Berechnungen

(* Messungen nach [Mül 92], — FEM)

 

Um die für die Signalgewinnung mittels DMS (K‑Faktor » 2) notwendigen Schwingungsamplituden in der Grö­ßen­ord­nung von einigen hundert Nanometern zu erzeugen, waren mittlere Impulsheizleistungen um 180 mW notwendig. Da die DMS‑Widerstände bei Anlegen einer Brückenspeisespannung zusätzliche Wärmequellen dar­stellen, ergeben sich, wie Infrarotmessungen zeigen, Temperaturüberhöhungen in Balkenmitte bis zu 60 K bei P_DMS = 650 mW. Gleichzeitig ändert sich die Temperatur des Keramikträgers, so daß aufgrund der unter­schied­lichen thermischen Ausdehnungs­koeffi­zien­ten zwischen Silizium und Keramik zusätzliche axiale Kräfte auf den Balken übertragen werden. Dieser Effekt ist bei der Interpretation des gemessenen, nicht-­monotonen Frequenzganges der Grundmode in Abhängigkeit von der in der Brücke umgesetzten elek­tri­schen Leistung mit zu beachten.

Die bei stetig zunehmender Brückenverlustleistung zu beobachtende Frequenzabnahme bis zu einem kritischen Wert von P_DMS, oberhalb dessen die Frequenz wieder zunimmt, läßt sich  mit dem “buckled‑beam”‑Modell nach [Bou 91] beschreiben. Unter der Grundannahme, daß ein an beiden Seiten fest eingespannter Balken unter Zugvorspannungen steht, die deutlich größer sein müssen als die aus der Biegesteifigkeit resultierende Spannung, folgt bei zu­neh­men­der Temperaturüberhöhung ΔT des Balkens gegenüber seiner Umgebung ein Abbau dieser Zug­span­­nungen durch Kom­pres­­sion und damit für eine kritische Temperaturdifferenz ΔT_kr eine Frequenzabnahme bis auf Null. Oberhalb dieser Temperaturdifferenz verändert sich die Biegelinie, so daß infolge Ausknickens der vorher gerade Balken verwölbt wird. Die dabei auftretenden Zugspannungen führen zu einer Zunahme der Reso­nanz­frequenz.

Ausgehend vom mathematischen Modellansatz in [Gei 91] wurden die folgenden analytischen Beziehungen zur Anpas­sung der experimentellen Werte abgeleitet:

>>> to be continued

wobei ΔT_kr = S/E×α ist und der thermische Ausdehnungskoeffizient von Silizium α = 2,33×10^‑6 1/K beträgt. Der freie Parameter S stellt die Summe der axialen Vorspannungen und die aus der Biegesteifigkeit resultierende Spannung dar.

 

Abb. 5 :  Abhängigkeit der Resonanzfrequenz der Grundmode von der in der DMS-Brücke umgesetzten elektrischen

Leistung (Balkenlänge: L = 10 mm, Impulsheizleistung: 180 mW, ° Meßpunkte nach [Wie 93], ––– FEM,

— analytisch gefittet nach Gleichungen (2) und (3))

 

Wird für den Zusammenhang zwischen Temperaturüberhöhung und elektrischer Verlustleistung ΔT = 0,084 P_DMS gesetzt, so ergibt sich eine gute Übereinstimmung für S » 12,1 MPa, was einer kritischen Temperaturdifferenz ΔT_kr von 30,6 K entspricht. Dieser Wert liegt erwartungsgemäß über dem aus FEM‑Berechnungen ermittelten Wert von 25,5 K, da im FE‑Modell keine Vorspannungen angenommen wurden. Berücksichtigt wurde hierbei neben der Temperatur­abhängigkeit der Materialparameter lediglich die aus den unterschiedlichen thermischen Ausdehnungs­koeffi­zien­ten von Silizium und SiO₂ resultierenden thermisch induzierten Spannungen. In Abb. 5 sind die experimentellen Werte, die an die Messungen analytisch angepaßten und die FE‑modellierten Kurvenverläufe dargestellt.

 

 

Sensitives Verhalten

Einwirkung einer Axialkraft

Die Kraftempfindlichkeit der Sensoren wurde im Niedertemperaturbereich (P_Heiz = 50 mW, P_DMS = 0) gemes­sen, wobei die Abtastung optisch erfolgte. Die Sensoren mit der Balkenlänge von 10 mm wiesen im Kraftbereich bis etwa 11 N eine Frequenzverschiebung von etwa 1820 Hz auf. Die Grundfrequenz betrug 4,265 kHz. Wird die Gesamt­quer­schnitts­­fläche der Sensoren (ca. 7,1×10^-7 m²) zugrunde gelegt, so entspricht dieses einer mechanischen Verspannung im Resonator von rund 15,3 MPa, so daß die gemessene Empfindlichkeit etwa 119 Hz/MPa beträgt.

Zur Überprüfung der FE-Modellannahmen wurde die Eigenfrequenzverschiebung unter der Einwirkung einer Axial­kraft berechnet. Durch die äußere Lasteinwirkung ergibt sich eine Überlagerung eines statischen und eines dynamischen Problems. Im ersten Schritt wird die Balkendehnung als Funktion der einwirkenden Last ermittelt, im zweitem Schritt die Frequenz­verschiebung in Abhängigkeit der Änderung der Resonatorsteifigkeit. Für eine Zugspannung von 15,2 MPa wurde eine Frequenzänderung von etwa 1,868 kHz berechnet, was einer Em­pfind­lich­keit von etwa 123 Hz/MPa ent­­spricht. Diese Werte stimmen gut miteinander überein, so daß die Modellannahmen bestätigt wurden und die Konsistenz des FE-Modells gegeben ist. Die Empfind­lichkeit der Sili­ziumbalken läßt sich durch eine geeignete Wahl der Querschnittsfläche der Verstär­kungs­stege (Rahmen) und der Balkendimensionen für Kraft­sensor­anwen­dungen in unterschiedlichen Kraftbereichen genau einstellen. In Abb. 6 sind die experimentellen und numerisch berech­neten Ergebnisse graphisch dargestellt.

 

 

Abb. 6 :  Abhängigkeit der Resonanzfrequenz von einer Axialkraft und der im Resonator auftretenden mechanischen

Spannung im Vergleich mit FEM-Berechnungen (° Meßwerte nach [Mül 92], ––– FEM)

 

 

Einfluß von Gasströmung: (thermisches Anemometerprinzip)

Ein auf einem Keramikzwischenträger montierter Sensor wurde in ein Strömungsrohr parallel zum Gasfluß (Luft) eingebaut und bei DMS‑Verlustleistungen unterhalb und oberhalb des mit der kritischen Temperatur­überhöhung kor­relierenden Wertes (180 mW) betrieben. In Abb. 7 sind die experimentell er­mit­telten Zusam­men­hänge von Frequenz­änderung und Fluidgeschwindigkeit dargestellt [Wie 93]. Charakteristisch ist, daß im Anfangsverlauf der Meßkurven (die Meßwerte wurden stets im thermischen Gleichgewicht aufgenommen) gerade ein gegenläufiges Verhal­ten der Reso­nanz­frequenzänderung beobachtet wird, als nach der Sensor­charak­teristik (Abb. 5) zu erwarten wäre. Erst oberhalb von etwa 1 m/s bewirkt die zunehmende Fluid­-Geschwin­digkeit eine Abkühlung, so daß für P_DMS < P_kr eine Fre­quenz­zunahme, für P_DMS > P_kr eine Frequenz­abnahme eintritt. Diese Beobachtung läßt sich qualitativ verstehen, wenn man berücksichtigt, daß der Keramik­zwischen­träger gleichfalls gekühlt wird. Aufgrund seines hohen thermischen Aus­dehnungs­koeffizienten bewirkt die Längenkontraktion eine axiale Druckkraft auf den Sensor, was partiell die Frequenzänderungen infolge des Anemometereffektes kompensiert.

 

 

 

Abb. 7 :  Abhängigkeit der Resonanzfrequenz von der Strömungsgeschwindigkeit:

a.) P_DMS = 150 mW < P_krit, b.) P_DMS = 330 mW > P_krit [Wie 93]

 

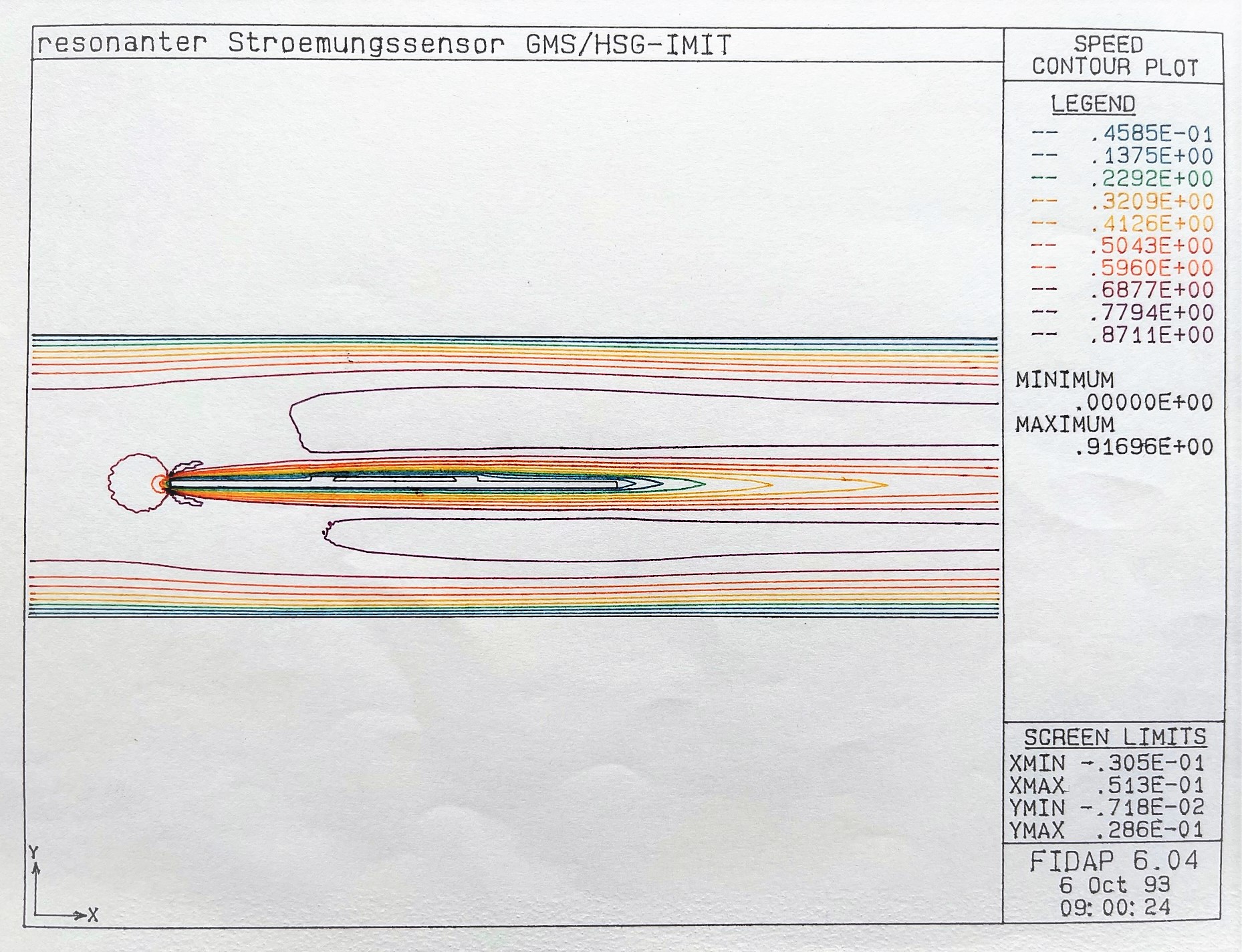
Um die thermische Wechselwirkung zwischen Resonator und dem umströmenden Fluid und die Auswirkung auf die Resonanzfrequenz zu untersuchen, wurde das Strömungsberechnungsprogramm FIDAP [FDI] mit dem Struk­tur­berech­nungs­­programm ANSYS [SASI] gekoppelt. Hierzu wurde die FE-Modellgeometrie mit den entsprechenden Rand­be­din­gun­gen in ANSYS definiert und die Temperaturen (T = 20°C) und Geschwindigkeiten am Eintritt des Strömungs­rohres als Anfangs­bedingungen vorgegeben. Anschließend erfolgte mit FIDAP die Berechnung der geschwin­dig­keits­abhängigen Temperaturverteilung, die als Eingabedaten für eine statische Temperaturanalyse an ANSYS wieder übergeben wurden. In einer nachfolgenden Modalanalyse wurden die Eigenfrequenzen des thermisch verspannten Balken­resonators ermittelt. Das zweidimen­sionale FE-Modell stellt einen Schnitt durch den Sensor und das Strömungsrohr dar und verwendet temperatur­abhän­gige Materialdaten für Silizum und den Keramik­substrat­träger. Die Berechnung erfolgte unter der Annahme laminarer und inkompressibler Strömung. In Abb. 8 ist die berechnete Temperaturverteilung im Fluid und dem Silizium-Resona­tor für eine mittlere Eintritts­geschwin­digkeit von 0,5 m/s dargestellt. Die mittlere Temperatur auf dem Siliziumbalken beträgt etwa 35°C, während der Keramikträger im vorderen Staupunkt um etwa 10°C abgekühlt wird.

 

 

 

Abb. 8 :  Berechnete Temperaturverteilung im Fluid (laminare Strömung: v = 0,5 m/s, T = 20°C)

 

 

In Abb. 9 ist die infolge der thermischen Fluid-Struktur-Wechselwirkung berechnete Abhängigkeit der Reso­­nanz­frequenz der Grundmode von der Strömungsgeschwindigkeit für niedrige Leistungen (P_DMS < P_krit) dar­gestellt. Die Resonanzfrequenzänderung df/dv beträgt bei der FEM-Berechnung etwa 1,5 kHz pro m/s (v = 0,2-1 m/s) und fällt im Gegensatz zu der Messung (Abb. 7 a: v = 1-3 m/s) um etwa eine Größenordnung höher aus. Zum einen liegt dies an der mecha­ni­schen Gegen­wirkung des Keramiksubstrates, die nur bei der Strömungs­simulation mit modelliert wurde, zum anderen an der nur ungenügend erfaßten Gesamtwärmebilanz des Sensors.

 

 

 

Abb. 9 :  FEM-Berechnung der Abhängigkeit der Resonanzfrequenz von der Strömungsgeschwindigkeit [Mes 93]

 

Zusammenfassung

Das Verfahren zur Herstellung der in diesem Beitrag beschriebenen frequenzanalogen Silizium‑Sensoren mit elektrothermischem Antrieb sichert eine hohe Kompatibilität der für das elektrische Layout durchgängig genutzten Metalldünnfilmtechnologie mit der Silizum‑Ätztechnologie. Damit sind gute Voraussetzungen für hohe Aus­beu­ten und niedrige Kosten gegeben. Die hohe thermische Stabilität des verwendeten Metallschichtsystems stellt einen Hochtemperatureinsatz (T > 150°C) in Aussicht.

 

Der elektrothermische Antrieb erlaubt abhängig von Impulsfolgefrequenz und Heizleistung ein stabiles Anregen der Resonatoren in Bereichen außerhalb der kritischen Temperaturüberhöhung.

 

Die Diskussion der experimentellen Ergebnisse zum Schwingungsverhalten und der Abhängigkeit der Resonanz­frequenz von Kraft und Gasströmung verdeutlichen den hohen Einfluß innerer Verspannungen und die Auswir­kun­gen der Aufbau- und Verbindungstechnik auf die Sensorcharakteristiken. Hier sind Schwerpunkte in einer weiteren angepaß­ten Sensor­entwicklung zu suchen, um die potentiell hohen Empfindlichkeiten eines solchen Resonators voll ausnutzen zu können.

 

Das Verhalten der Resonatoren wurde sowohl analytisch  (“buckled-beam”‑Modell) als auch mittels FE‑Modellierung in guter Übereinstimmung mit den experimentellen Ergebnissen beschrieben. Die Strömungsberechnungen haben aller­dings eher qualitativen Charakter, so daß quantitative Aussagen Gegenstand weiterer Untersuchungen sein müssen.

 

Anmerkung

Die vorgestellten Arbeiten wurden im Rahmen des Verbundvorhabens “Einsatz der Mikromechanik zur Her­stel­lung frequenzanaloger Sensoren” vom Bundes­ministerium für Forschung und Technologie (BMFT) unter den Förder­kenn­zeichen 13 AS  0114 / 161A durchgeführt.

 

Literaturverzeichnis

• [Bou 90] : S. Bouwstra, Resonating microbridges mass flow sensor, Dissertation, Universität von Twente, Enschede, Niederlande (1990)
• [Bou 91] : S. Bouwstra, B. Geijselaers, On the resonance frequencies of microbridges, Proc. TRANSDUCERS (1991) 538‑542
• [Bra 92] : C. Braxmaier, Fremdanregung von Balken durch Dickenschwinger zur Eigenfrequenz­bestimmung, Praktikums­arbeit, HSG-IMIT, VS-Villingen (1992)
• [Duf 92] : M. Dufour, M.T. Delaye, F. Michel, J.S. Danel, B. Diem, G. Delapierre, A comparsion between micro­machined pressure sensors using quartz or silicon vibrating beams, Sensors and Actuators A, 34 (1992) 201‑209
• [FDI] :Fluid Dynamics International, Inc., Evanston, Illinois, USA
• [Gei 91] : H.J.M. Geijselaers, H. Tijdeman, The dynamic mechanical characteristics of a resonating microbridge mass-flow sensor, Sensors and Actuators A, 29 (1991) 37-41
• [Mes 93] : S. Messner, Finite-Elemente Berechnung der Fluid-Struktur-Wechselwirkung bei einem mikromechanischen Strömungssensor, Diplomarbeit, Universität Stuttgart/HSG-IMIT, VS-Villingen (in Vorbereitung)
• [Mur 92] : H. Muro, H. Kaneko, S. Kiyota, P.J. French, Stress analysis of SiO₂/Si bi-metal effect in silicon accelerometers and its compensation, Sensors and Actuators A, 34 (1992) 43-49
• [Mül 92] : M. Müller, Aufbau und Inbetriebnahme eines optischen Meßplatzes zur Charakterisierung von resonanten mikromechanischen Strukturen, Diplomarbeit, FH-Furtwangen (1992)
• [SASI] : Swanson Analysis Systems, Inc., Houston, PA, USA
• [Wie 93] : M.‑C. Wiedemann, Entwicklung von Anregungsschaltungen für frequenzanaloge Sensoren, Diplomarbeit, FH-Kiel (in Vorbereitung)

 

GitHub repository

Link: github.com/ThomasFabula/Flow

 

Testimonial

“One of Dr. Fabula’s tasks was to optimize the design of pressure transducers with metal film strain gauges by means of FE calculations. The results obtained were successful in industrial practice and helped to stabilize and further develop this production line at GMS.

Dr. Fabula also demonstrated his technical expertise, combined with prudent work organization and a high level of commitment in other projects. His work on modelling and application-specific optimization of micromechanical force and flow sensors using the FE method had a decisive influence on the design and layout of prototypes of a micromechanical force sensor with electrothermal excitation which were then manufactured at GMS.

On the initiative of Dr. Fabula, GMS decided to continue the work on a marketable product in a joint project. The results are reflected in the customer-specific development currently underway at our company.

Dr. Fabula always proved to be very open to the specific development tasks of our company. We would like to thank him for his services to date and look forward to continuing our good cooperation.” ~ Dipl.-Ing. Hans Weiss | Owner & Managing Director, GMS Gesellschaft für Mikroelektronik und Sensorik mbH, VS-Villingen

Dipl.-Ing. Hans Weiss | GMS Gesellschaft für Mikroelektronik und Sensorik mbH, VS-Villingen

Sensoren mit elektrothermischer Anregung